动物PET的采集转换、排序与符合算法
本工程主要负责将读入的chnnel原始数据,根据位置谱与能量谱,进行类型转化,得到位置信息、时间信息与能量信息,并根时间信息进行排序,主要是采用GPU归并排序进行快速排序,为后面的时间符合做准备。
文章目录
- 动物PET的采集转换、排序与符合算法
- 输入输出结构描述
- 输入数据描述
- 输出数据描述
- 转换算法
- 算法思路
- 核函数实现
- 排序
- 算法流程
- 代码实现
- 符合
- 算法思路
- 重要核函数
- calcDataBlockLength
- intraBlockScan
- intraWarpScan
输入输出结构描述
输入数据描述
1. typedef struct _DataFrameV2
2. {
3. uint8 nHeadAndDU;
4. uint8 nBDM;
5. uint8 nTime[8];
6. uint8 x;
7. uint8 y;
8. uint8 Energy[2];
9. int8 nTemperatureInt;
10. uint8 nTemperatureAndTail;
11. } DataFrameV2;
输出数据描述
1. typedef struct _SinglesStruct
2. {
3. uint32 globalCrystalIndex;
4. float energy;
5. double timevalue;
6. }SinglesStruct;
转换算法
算法思路
主要是在原本的CPU算法上实现了并行化,默认进行能量符合,默认一个线程块启动128个线程,一个线程处理32个数据进行转换(参数可调整)。
1.如果进行能量符合,那么每一个线程中会用一个变量去记录当前线程处理的元素进行类型转换以后通过能量符合的数据个数,程序中表现为localTrue;再利用warp的特性,调用intraBlockScan函数,可以得到在这个线程块内,每个线程之前(包括本线程)的所有线程中可以通过能量符合的数据个数,再利用原子操作atomicAdd,得到每个线程块的起始位置,则可以通过计算得到,每一个线程块需要放置通过能量符合元素的起始位置,在程序中表现为indexTrue,则可以将通过能量符合的数据放到自己在dst中对应的位置,并可以得到总共数据的长度*coinEnergyLength。
2.如果没有进行能量符合,那么每一个数据都不会被筛选掉,在src中的位置取出,会被放到dst中对应的位置。
核函数实现
template <unsigned threadsConvert, unsigned elemsConvert>
__global__ void convertUdpToSinglesKernel(DataFrameV2* src, SinglesStruct* dst, SinglesStruct* dstBuffer, unsigned arrayLength, const CoinPetPara mCoinPetPara, uint8* d_m_pPositionTable, float* d_m_pEnergyCorrFactor, bool mIsCoinEnergy, unsigned* coinEnergyLength) {
unsigned offset, dataBlockLength;
calcDataBlockLength<threadsConvert, elemsConvert>(offset, dataBlockLength, arrayLength); // 找到每个线程块操作元素的偏移量和长度
/* Position, Energy, Time corrections included */
unsigned m_nChannelNum = mCoinPetPara.m_nChannelNum;
// unsigned moduleNumX = mCoinPetPara.m_nModuleNumX;
unsigned moduleNumY = mCoinPetPara.m_nModuleNumY;
// unsigned moduleNumZ = mCoinPetPara.m_nModuleNumZ;
// unsigned blockNumX = mCoinPetPara.m_nBlockNumX;
unsigned blockNumY = mCoinPetPara.m_nBlockNumY;
unsigned blockNumZ = mCoinPetPara.m_nBlockNumZ;
// unsigned crystalNumX = mCoinPetPara.m_nCrystalNumX;
unsigned crystalNumY = mCoinPetPara.m_nCrystalNumY;
unsigned crystalNumZ = mCoinPetPara.m_nCrystalNumZ;
unsigned positionSize = mCoinPetPara.m_nPositionSize;
unsigned localTrue = 0;
unsigned scanTrue = 0;
for (unsigned tx = threadIdx.x; tx < dataBlockLength; tx += threadsConvert) {
/* Temporary structure to provide BDM and DU info */
// 临时结构,提供BDM和DU信息
TempSinglesStruct temp;
temp.globalBDMIndex = src[offset + tx].nBDM;
temp.localDUIndex = src[offset + tx].nHeadAndDU & (0x0F); // 为什么要取与运算(截去前8个位,留下后面8个位)
/* Time convertion, from unsigned char[8] to double */
// 时间转换,从unsigned char[8]到double
uint64 nTimeTemp;
nTimeTemp = src[offset + tx].nTime[0];
for (unsigned i = 1; i <= 7; ++i) {
nTimeTemp <<= 8; // 将8个8位数据转换为一个64位数据
nTimeTemp |= src[offset + tx].nTime[i];
}
temp.timevalue = (double)nTimeTemp;
/* Position correction */
// 位置校正(这里是怎么样的结构,在计算什么)
uint32 originCrystalIndex = (d_m_pPositionTable + temp.globalBDMIndex * mCoinPetPara.m_nDUNum * mCoinPetPara.m_nPositionSize * mCoinPetPara.m_nPositionSize +
temp.localDUIndex * mCoinPetPara.m_nPositionSize * mCoinPetPara.m_nPositionSize)[src[offset + tx].X + src[offset + tx].Y * positionSize];
uint32 localX = originCrystalIndex % crystalNumZ;
uint32 localY = originCrystalIndex / crystalNumY;
temp.localCrystalIndex = localX + (crystalNumY - 1 - localY) * crystalNumZ;
/* Time correction */
/* Energy convertion, from unsigned char[2] to float */
uint32 nEnergyTemp;
nEnergyTemp = (src[offset + tx].Energy[0] << 8 | src[offset + tx].Energy[1]); // 将两个能量进行合并
temp.energy = (float)nEnergyTemp;
/* Up to different system structure ||Changeable|| */
//uint32 nCrystalIdInRing = temp.globalBDMIndex % m_nChannelNum * m_nCrystalSize + (m_nCrystalSize - temp.localCrystalIndex / m_nCrystalSize -1);
//uint32 nRingId = temp.localDUIndex % m_nDUNum * m_nCrystalSize + temp.localCrystalIndex % m_nCrystalSize;
//uint32 nCrystalNumOneRing = m_nCrystalSize * m_nChannelNum;
uint32 nCrystalIdInRing = temp.globalBDMIndex % (m_nChannelNum * moduleNumY) * blockNumY * crystalNumY + temp.localDUIndex / blockNumZ * crystalNumY + temp.localCrystalIndex / crystalNumZ;
uint32 nRingId = temp.globalBDMIndex / (m_nChannelNum * moduleNumY) * blockNumZ * crystalNumZ + temp.localDUIndex % blockNumZ * crystalNumZ + temp.localCrystalIndex % crystalNumZ;
uint32 nCrystalNumOneRing = crystalNumY * blockNumY * m_nChannelNum;
dstBuffer[offset + tx].globalCrystalIndex = nCrystalIdInRing + nRingId * nCrystalNumOneRing;
/* Energy correction */
// 能量校正
dstBuffer[offset + tx].energy = temp.energy * (d_m_pEnergyCorrFactor + temp.globalBDMIndex * mCoinPetPara.m_nDUNum * mCoinPetPara.m_nCrystalSize * mCoinPetPara.m_nCrystalSize * 1000 +
temp.localDUIndex * mCoinPetPara.m_nCrystalSize * mCoinPetPara.m_nCrystalSize * 1000 +
temp.localCrystalIndex * 1000)[int(floor(temp.energy / 10))];
dstBuffer[offset + tx].timevalue = temp.timevalue;
// 这里要进行能量的筛选和合并
// TODO: THE RIGHT PLACE FOR COIN ENERGY!
// 计算每个线程操作的元素中能量满足要求的元素个数
localTrue += coinEnergyKernel(dstBuffer[offset + tx].energy, mCoinPetPara);
}
// 针对每个线程块的操作不同
// 得到这个线程块内,每个线程之前(包括该线程)的所有线程中为TRUE的元素个数
scanTrue = intraBlockScan<threadsConvert>(localTrue);
__syncthreads();
__shared__ unsigned globalTrue;
if (threadIdx.x == (threadsConvert - 1)) // 每个线程块中的最后一个线程,此线程中scanLower存放的是本线程块中小于pivots的元素总数
{
globalTrue = atomicAdd(coinEnergyLength, scanTrue); // 原子操作,必须一个个进行
}
__syncthreads();
unsigned indexTrue = globalTrue + scanTrue - localTrue; // 每个线程中小于pivots要存入的起始位置
for (unsigned tx = threadIdx.x; tx < dataBlockLength; tx += threadsConvert) // 这里完成合并操作
{
SinglesStruct temp = dstBuffer[offset + tx]; // 取出每一个要处理的元素
if (coinEnergyKernel(temp.energy, mCoinPetPara))
{
dst[indexTrue++] = temp;
}
}
}
排序
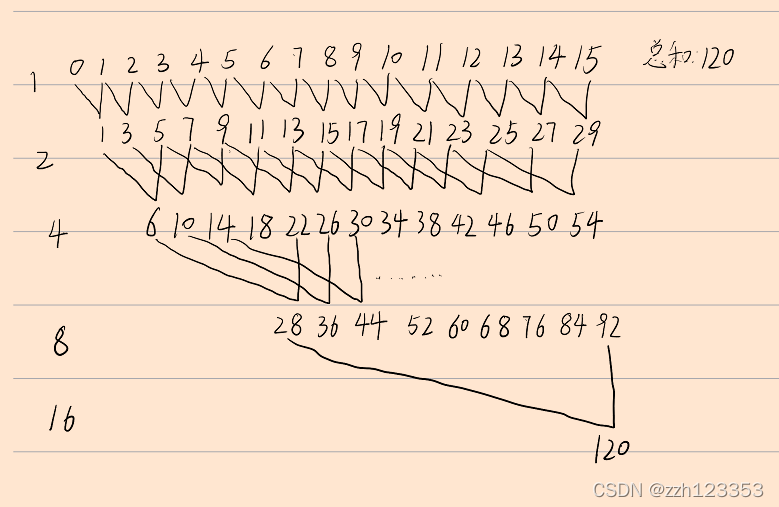
主要采用了GPU归并排序,主要分为3步:
1.填充数据(成为2的整数幂)
2.局部有序
3.全局有序
算法流程
1.如果数据长度不是2的整次幂,需要把数据长度扩充到下一个2的整次幂,填充最大值,更加方便后续操作,并行填充数据。
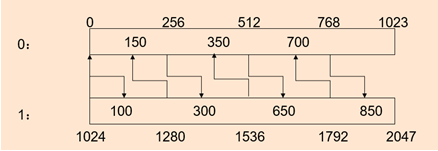
2.然后让数据局部有序,调用runMergeSortKernel函数,让数据进行局部有序,分别计算当前元素在另一块数据中的位置,再加上当前的位置,则可以得到它应该放入的位置,为了防止位置找重,一块中的数据寻找在另一块中小于当前元素的位置,另一块中数据寻找在这一块中不小于当前元素的位置,那么最终就可以得到局部有序的数据。在代码中默认是每1024个数据有序。
3.最后让局部有序的部分逐渐合并,主要是生成多个块,每一个块取一个端点值,块与块之间默认间隔256,每个块的端点值负责寻找在另一个需要合并的数据中的位置,然后将块中的元素根据上面的一样的思路进行合并,最终可以得到完全有序的数据。
代码实现
外部框架:
void parallelMergeSort(SinglesStruct* dst, SinglesStruct* dstBuffer, unsigned arrayLength) {
unsigned* d_ranksEven = NULL;
unsigned* d_ranksOdd = NULL;
unsigned elemsPerThreadBlock = THREADS_MERGESORT * ELEMS_MERGESORT;
unsigned arrayLenRoundedUp = max(nextPowerOf2(arrayLength), elemsPerThreadBlock);
unsigned ranksLength = (arrayLenRoundedUp - 1) / SUB_BLOCK_SIZE + 1; // 求出子块的数目
cudaError_t error;
error = cudaMalloc((void**)&d_ranksEven, 2 * ranksLength * sizeof(*d_ranksEven));
checkCudaError(error);
error = cudaMalloc((void**)&d_ranksOdd, 2 * ranksLength * sizeof(*d_ranksOdd));
checkCudaError(error);
unsigned sortedBlockSize = THREADS_MERGESORT * ELEMS_MERGESORT;
unsigned lastPaddingMergePhase = log2((double)(sortedBlockSize)); // 计算合并阶段
unsigned arrayLenPrevPower2 = previousPowerOf2(arrayLength);
addPadding(dst, dstBuffer, arrayLength); // 两个数组都填满2的幂次(可能会导致越界) 第一步
runMergeSortKernel(dst, arrayLength); // data局部有序,databuffer无序 每1024个元素有序 第二步
//第三步
while (sortedBlockSize < arrayLength)
{
SinglesStruct* temp = dst;
dst = dstBuffer;
dstBuffer = temp;
lastPaddingMergePhase = copyPaddedElements( // 判断剩余部分是否需要参与排序,如果需要排序,是否应该进行数据转移,并记录最近一次剩余部分参与排序的阶段
dst + arrayLenPrevPower2, dstBuffer + arrayLenPrevPower2,
arrayLength, sortedBlockSize, lastPaddingMergePhase
);
runGenerateRanksKernel(dstBuffer, d_ranksEven, d_ranksOdd, arrayLength, sortedBlockSize); //生成带记录的各个块
runMergeKernel(dstBuffer, dst, d_ranksEven, d_ranksOdd, arrayLength, sortedBlockSize); //按照次序进行合并
sortedBlockSize *= 2;
}
error = cudaFree(d_ranksEven);
checkCudaError(error);
error = cudaFree(d_ranksOdd);
checkCudaError(error);
}
生成带记录的各个块的位置核函数:
template <unsigned subBlockSize>
__global__ void generateRanksKernel(SinglesStruct* data, unsigned* ranksEven, unsigned* ranksOdd, unsigned sortedBlockSize)
{
unsigned subBlocksPerSortedBlock = sortedBlockSize / subBlockSize; // 每个有序数组划分成多少个子块
unsigned subBlocksPerMergedBlock = 2 * subBlocksPerSortedBlock; // 两个合并的排序数组的子块总数
// 找到要处理的端点值
SinglesStruct sampleValue = data[blockIdx.x * (blockDim.x * subBlockSize) + threadIdx.x * subBlockSize]; // 注意一个线程查找一个端点
unsigned rankSampleCurrent = blockIdx.x * blockDim.x + threadIdx.x; // 端点号
unsigned rankSampleOpposite;
// 找到该端点号(子块)所在的序列以及它的相对应序列
unsigned indexBlockCurrent = rankSampleCurrent / subBlocksPerSortedBlock; // 端点号对应的序列
unsigned indexBlockOpposite = indexBlockCurrent ^ 1; // 相对应要处理的序列
// 找到这个端点值在相对应序列的哪个子块
if (indexBlockCurrent % 2 == 0)
{
rankSampleOpposite = binarySearchInclusive<subBlockSize>( // 有步幅的二分查找
data, sampleValue, indexBlockOpposite * sortedBlockSize, // 查找端点在另一个序列中的位置
indexBlockOpposite * sortedBlockSize + sortedBlockSize - subBlockSize
);
rankSampleOpposite = (rankSampleOpposite - sortedBlockSize) / subBlockSize; // 相对位置
}
else
{
rankSampleOpposite = binarySearchExclusive<subBlockSize>(
data, sampleValue, indexBlockOpposite * sortedBlockSize,
indexBlockOpposite * sortedBlockSize + sortedBlockSize - subBlockSize
);
rankSampleOpposite /= subBlockSize;
}
// 计算合并块内的样本索引
unsigned sortedIndex = rankSampleCurrent % subBlocksPerSortedBlock + rankSampleOpposite; // 所在块编号
// 计算样本在当前和相对排序块中的位置
unsigned rankDataCurrent = (rankSampleCurrent * subBlockSize % sortedBlockSize) + 1; // 在当前序列中的相对位置+1
unsigned rankDataOpposite;
// 计算相对排序块内的子块索引(这里缩小了查找范围)
unsigned indexSubBlockOpposite = sortedIndex % subBlocksPerMergedBlock - rankSampleCurrent % subBlocksPerSortedBlock - 1;
unsigned indexStart = indexBlockOpposite * sortedBlockSize + indexSubBlockOpposite * subBlockSize + 1; // 不取端点值
unsigned indexEnd = indexStart + subBlockSize - 2;
if ((int)(indexStart - indexBlockOpposite * sortedBlockSize) >= 0)
{
if (indexBlockOpposite % 2 == 0) // 本身是奇序列
{
rankDataOpposite = binarySearchExclusive( // 二分查找位置
data, sampleValue, indexStart, indexEnd // 满足条件的后面一个位置(这样保证了两个序列中存在两个相同的数字时也可以满足)
);
}
else // 本身是偶序列
{
rankDataOpposite = binarySearchInclusive(
data, sampleValue, indexStart, indexEnd // 满足条件的位置
);
}
rankDataOpposite -= indexBlockOpposite * sortedBlockSize;
}
else
{
rankDataOpposite = 0;
}
// 对应的每个子块结束位置
if ((rankSampleCurrent / subBlocksPerSortedBlock) % 2 == 0) // 本身是偶序列
{
ranksEven[sortedIndex] = rankDataCurrent; // 这里多加了1,保证至少有一个元素参与合并
ranksOdd[sortedIndex] = rankDataOpposite;
}
else
{
ranksEven[sortedIndex] = rankDataOpposite;
ranksOdd[sortedIndex] = rankDataCurrent; // 这里多加了1
}
}
进行合并核函数:
//合并由rank数组决定的连续的偶数和奇数子块。
template <unsigned subBlockSize>
__global__ void mergeKernel(
SinglesStruct* data, SinglesStruct* dataBuffer, unsigned* ranksEven, unsigned* ranksOdd, unsigned sortedBlockSize
)
{
__shared__ SinglesStruct tileEven[subBlockSize]; // 每个子块的元素个数不超512
__shared__ SinglesStruct tileOdd[subBlockSize]; // 子块中奇子块和偶子块的元素个数均不超过256
unsigned indexRank = blockIdx.y * (sortedBlockSize / subBlockSize * 2) + blockIdx.x; // 找到当前线程块对应的子块
unsigned indexSortedBlock = blockIdx.y * 2 * sortedBlockSize; // 该线程块操作的子块所在的序列的操作的起始位置
// 索引相邻的偶数和奇数块,它们将被合并
unsigned indexStartEven, indexStartOdd, indexEndEven, indexEndOdd;
unsigned offsetEven, offsetOdd;
unsigned numElementsEven, numElementsOdd;
// 读取偶数和奇数子块的START索引
// 每个线程块操作相同的起始和结束位置
if (blockIdx.x > 0)
{
indexStartEven = ranksEven[indexRank - 1];
indexStartOdd = ranksOdd[indexRank - 1];
}
else
{
indexStartEven = 0;
indexStartOdd = 0;
}
// 读取偶数和奇数子块的END索引
if (blockIdx.x < gridDim.x - 1)
{
indexEndEven = ranksEven[indexRank];
indexEndOdd = ranksOdd[indexRank];
}
else // 序列对应的最后一个线程块
{
indexEndEven = sortedBlockSize; // 最后一个序列
indexEndOdd = sortedBlockSize;
}
numElementsEven = indexEndEven - indexStartEven; // 求出该线程块操作的元素个数
numElementsOdd = indexEndOdd - indexStartOdd;
// 从偶数有序子块中读取数据
if (threadIdx.x < numElementsEven)
{
offsetEven = indexSortedBlock + indexStartEven + threadIdx.x;
tileEven[threadIdx.x] = data[offsetEven];
}
// 从奇数有序子块中读取数据
if (threadIdx.x < numElementsOdd)
{
offsetOdd = indexSortedBlock + indexStartOdd + threadIdx.x;
tileOdd[threadIdx.x] = data[offsetOdd + sortedBlockSize];
}
__syncthreads();
if (threadIdx.x < numElementsEven)
{
unsigned rankOdd = binarySearchInclusive(tileOdd, tileEven[threadIdx.x], 0, numElementsOdd - 1);
rankOdd += indexStartOdd;
// 求出在全局数组中的位置
dataBuffer[offsetEven + rankOdd] = tileEven[threadIdx.x];
}
if (threadIdx.x < numElementsOdd)
{
unsigned rankEven = binarySearchExclusive(tileEven, tileOdd[threadIdx.x], 0, numElementsEven - 1);
rankEven += indexStartEven;
dataBuffer[offsetOdd + rankEven] = tileOdd[threadIdx.x];
}
}
符合
符合主要引入了时间窗的概念,当一个时间窗内只有两个事件的时候,并且这两个事件的全局晶体编号不一致,才能够生成一个符合对,否则将被全部剔除!
算法思路
在这里,我运用了四个核函数进行求解,
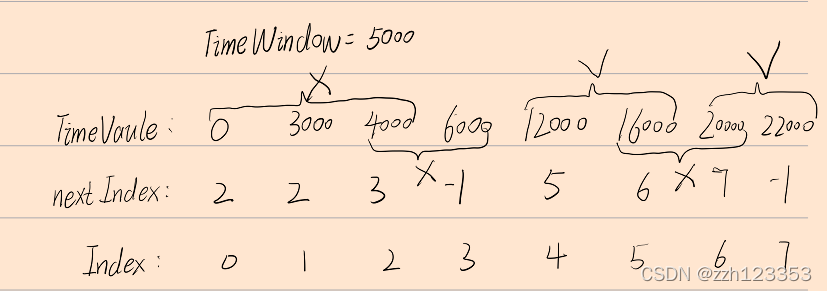
第一步:找到能和该事件匹配的下一个事件的位置,并存放在nextIdex中;
第二步:进行筛选,找到上一个相邻的两个事件时间差大于时间窗的位置记作left,可以找到的话则pos=left,找不到的话,则pos=offset+tx,即为自身起点,这个位置便是起始判断的位置,如果nextIndex[pos]-pos>=2时候,说明该事件窗内存在多个(>2个)事件,则需要进行剔除,将这个范围内的所有nextIndex全部抹成-1,表示无法配对,如果nextIndex[pos]-pos==1,则说明pos位置的事件可以与pos+1进行配对,则将nextIndex[pos+1]抹成-1;则最后只有可以配对的元素nextIndex里面存有有意义的值,无法配对的全部是-1;
第三步,进行配对,同样利用intraBlockScan函数,计算位置;
第四步,每个线程求取它该存放的位置,并进行放置数据,完成符合操作!
第一步代码实现:
inline __device__ int searchIndex(SinglesStruct* data, unsigned curIndex, unsigned arrayLength)
{
unsigned next = curIndex + 1;
while (next < arrayLength && data[next].timevalue - data[curIndex].timevalue <= TIMEWINDOW) { ++next; }
return next == curIndex + 1 ? -1 : next - 1;
}
inline __global__ void CoinTimeKernel(SinglesStruct* data, int* nextIndex, unsigned arrayLength) {
unsigned offset, dataBlockLength;
calcDataBlockLength<THREAD_NUM, THREAD_ELEM>(offset, dataBlockLength, arrayLength);
//每个线程找到满足时间窗口的最右边的index放到nextIndex数组中
//每个线程找到距它最远的满足每两个元素时间窗口都小于timewindow
for (unsigned tx = threadIdx.x; tx < dataBlockLength; tx += THREAD_NUM) {
nextIndex[tx + offset] = searchIndex(data, offset + tx, arrayLength);
}
}
第二步:
inline __device__ int leftIndex(SinglesStruct* data, unsigned curIndex)
{
int left = curIndex - 1;
unsigned pos = curIndex;
while (left >= 0 && data[curIndex].timevalue - data[left].timevalue <= TIMEWINDOW) { --curIndex; --left;}
return curIndex == pos ? -1 : curIndex;
}
inline __global__ void SelectKernel( SinglesStruct* data,int* nextIndex, unsigned* scanId, unsigned* globalLen, unsigned arrayLength) {
unsigned offset, dataBlockLength;
calcDataBlockLength<THREAD_NUM, THREAD_ELEM>(offset, dataBlockLength, arrayLength);
找到最左端的起点
for (unsigned tx = threadIdx.x; tx < dataBlockLength; tx += THREAD_NUM) {
int pos;
int left = leftIndex(data, tx + offset);
if (left != -1) {
pos = left; //左边起点
}
else {
pos = tx + offset; //起点是自身
}
if (nextIndex[tx + offset] == -1 && pos != tx + offset) {
while (pos <= offset + tx) {
if ((nextIndex[pos] - pos) >= 2) {
int begin = pos;
int end = nextIndex[pos];
for (; begin <= end; ++begin) {
nextIndex[begin] = -1;
}
pos = begin;
}
else if ((nextIndex[pos] - pos) == 1) {
if (data[pos].globalCrystalIndex == data[nextIndex[pos]].globalCrystalIndex) {
nextIndex[pos] = -1;
}
nextIndex[++pos] = -1; //++pos位置是事件对中的第二个
++pos;
}
else if (nextIndex[pos] == -1) {
++pos;
}
}
}
}
}
第三步:
inline __global__ void FillDataKernel(SinglesStruct* d_SingleData, CoinStruct* d_CoinData, int* nextIndex, unsigned arrayLength, unsigned* newLength, unsigned* scanId, unsigned* globalLen) {
unsigned offset1, dataBlockLength1;
unsigned local1 = 0, scan1 = 0;
unsigned id = threadIdx.x + blockDim.x * blockIdx.x;
__shared__ unsigned global1;
unsigned index = threadIdx.x + blockDim.x * blockIdx.x;
if (index * THREAD_ELEM < arrayLength) {
offset1 = index * THREAD_ELEM;
dataBlockLength1 = offset1 + THREAD_ELEM <= arrayLength ? THREAD_ELEM : arrayLength - offset1; //特殊处理最后一块
}
else {
return;
}
for (unsigned tx = 0; tx < dataBlockLength1; ++tx) {
if (nextIndex[tx + offset1] != -1) {
local1++;
}
}
__syncthreads();
scan1 = intraBlockScan<THREAD_NUM>(local1);
__syncthreads();
if (threadIdx.x == THREAD_NUM - 1 || offset1 + dataBlockLength1 == arrayLength) {
atomicAdd(newLength, scan1);
//globalPos[blockIdx.x] = atomicAdd(newLength, scan1);
globalLen[blockIdx.x] = scan1;
}
__syncthreads();
scanId[id] = scan1 - local1;
}
第四步:
inline __global__ void CorrectPosKernel(SinglesStruct* d_SingleData, CoinStruct* d_data, unsigned* newLength, unsigned* scanId, unsigned* globalLen, unsigned arrayLength, int* nextIndex) {
unsigned offset1, dataBlockLength1;
unsigned global = 0;
unsigned index = threadIdx.x + blockDim.x * blockIdx.x;
if (index * THREAD_ELEM < arrayLength) {
offset1 = index * THREAD_ELEM;
dataBlockLength1 = offset1 + THREAD_ELEM <= arrayLength ? THREAD_ELEM : arrayLength - offset1; //特殊处理最后一块
}
else {
return;
}
for (int i = 0; i < blockIdx.x; ++i) {
global += globalLen[i];
}
unsigned localBegin = global + scanId[index];
for (unsigned tx = 0; tx < dataBlockLength1; ++tx) {
if (nextIndex[tx + offset1] != -1) {
d_data[localBegin].nCoinStruct[0] = d_SingleData[tx + offset1];
d_data[localBegin++].nCoinStruct[1] = d_SingleData[tx + offset1 + 1];
}
}
}
重要核函数
calcDataBlockLength
Fuc:计算出每个线程的位置偏移,以及处理的元素的个数,需要对最后一块进行特殊处理
template <unsigned numThreads, unsigned elemsThread>
inline __device__ void calcDataBlockLength(unsigned& offset, unsigned& dataBlockLength, unsigned arrayLength)
{
unsigned elemsPerThreadBlock = numThreads * elemsThread; // 计算每个线程块要处理的数据量
offset = blockIdx.x * elemsPerThreadBlock;
dataBlockLength = offset + elemsPerThreadBlock <= arrayLength ? elemsPerThreadBlock : arrayLength - offset; // 对最后一个线程块的特殊处理
}
intraBlockScan
Func:算出来本线程块中满足条件的元素总个数,需要配合intraWarpScan使用。
算法大概流程: 其中val为每一个线程符合要求的元素个数,利用每32个线程组成一个warp的性质,求取该线程在第几个warp中的第几个位置,然后利用intraWarpScan可以得到每个warp中在这个位置之前的所有元素的个数总和,即每一个warp中的最后一个线程都记录了本warp中满足要求的所有数据的个数,然后可以单独让前几个位置去存放每个warp中满足要求的总元素的个数,例如:scanTile[0]存放第一个warp中满足要求元素总个数,scanTile[1]存放第二个warp中满足要求元素总个数等等,然后再对前面存放好的数据进行类似的操作,则scanTile[0]=0, scanTile[1]=第一个warp中满足要求总元素的个数,scanTile[2]= 第一个warp中满足要求总元素的个数+第二个warp中满足要求总元素的个数等等以此类推,最终的返回值即为在本线程之前(包括本线程的)所有满足要求的元素的个数,如果本线程是块中的最后一个线程,那么它的返回值则是整个块中所有满足要求的元素的个数!
template <unsigned blockSize>
inline __device__ unsigned intraBlockScan(unsigned val) {
__shared__ unsigned scanTile[blockSize * 2];
unsigned warpIdx = threadIdx.x / WARP_SIZE;
unsigned laneIdx = threadIdx.x & (WARP_SIZE - 1); // Thread index inside warp
unsigned warpResult = intraWarpScan<blockSize>(scanTile, val);
__syncthreads();
if (laneIdx == WARP_SIZE - 1) // 得到32个值的总和放在对应的warpIdx中
{
scanTile[warpIdx] = warpResult + val;
}
__syncthreads();
if (threadIdx.x < WARP_SIZE) // 仅用其中一个warp进行操作
{
scanTile[threadIdx.x] = intraWarpScan<blockSize / WARP_SIZE>(scanTile, scanTile[threadIdx.x]);
}
__syncthreads();
return warpResult + scanTile[warpIdx] + val;
}
intraWarpScan
Func:计算出本Warp中该线程之前(不包括该线程)的满足要求的元素的个数
template <unsigned blockSize>
inline __device__ unsigned intraWarpScan(volatile unsigned* scanTile, unsigned val) {
unsigned index = 2 * threadIdx.x - (threadIdx.x & (min(blockSize, WARP_SIZE) - 1));
scanTile[index] = 0; // 将前面一列置零
index += min(blockSize, WARP_SIZE);
scanTile[index] = val;
if (blockSize >= 2)
{
scanTile[index] += scanTile[index - 1];
}
if (blockSize >= 4)
{
scanTile[index] += scanTile[index - 2];
}
if (blockSize >= 8)
{
scanTile[index] += scanTile[index - 4];
}
if (blockSize >= 16)
{
scanTile[index] += scanTile[index - 8];
}
if (blockSize >= 32)
{
scanTile[index] += scanTile[index - 16];
}
// 多个元素的值进行合并
return scanTile[index] - val;
}
类似Reduce求解: