比赛链接
注:以下顺序为期望难度顺序
I. 中国人不骗中国人
- tag: 转义字符
直接输出即可,注意字符\的转义
参考代码:
#include <stdio.h>
int main(){
printf("I Love ecjtuacm /\\=/\\")
return 0;
}
C. 新年快乐
- tag: 阅读理解
仔细阅读题意即可发现,始终能得到最大的点数,并且点数不存在相同的情况。所以答案为
n
−
1
n-1
n−1
参考代码:
#include <stdio.h>
int main(){
int n;
while(~scanf("%d", &n)) {
int x;for(int i = 1; i <= n; ++ i) scanf("%d", &x);
printf("%d\n", n - 1);
}
return 0;
}
K. 一个寻找爱情的Acmer
- tag: 字符串处理
找出3的相对位置,特别的,第一个3原来是什么位置就是多少(字符串下标从1开始)。先找到第一个3,然后记录一下上一个3出现的位置。输出了8个就退出
参考代码:
#include <stdio.h>
#include <string.h>
char s[330];
int main()
{
int n;
scanf("%d", &n);
while(n --) {
scanf("%s", s + 1); // 下标从1开始
int len = strlen(s + 1);
int pre = 0, cnt = 0; // 上一个3的位置, 输出的数量
for(int i = 1; i <= len; ++ i) {
if(s[i] == '3') {
if(pre == 0) printf("%d", i);
else printf("%d", i - pre);
pre = i;
cnt ++;
if(cnt == 8) break;
}
}
printf("\n");
}
return 0;
}
F. 爱教书的赵哥哥
- tag: 结构体,排序
我们可以使用结构体来存储信息(当然只用数组也可以,只要你不会晕)。然后按照成绩排序得到一个新排名,记录以下进步以及退步(注意不进不退的不要管),最后按照要求输出就好啦。本题排序可以使用sort排序,也可以用上课讲的冒泡排序(按照成绩排序)具体的参考代码:
#include <stdio.h>
struct student{
int pre, grade, now, dex; // 之前的排名,现在的成绩 现在的排名
};
student a[22];
int main()
{
int t; scanf("%d", &t);
while(t -- ) {
int n; scanf("%d", &n);
for(int i = 1; i <= n; ++ i) {
scanf("%d", &a[i].grade);
a[i].pre = i; // 之前的排名就是顺序
}
// 接下来排序
for(int i = 1; i <= n; ++ i) {
for(int j = i + 1; j <= n; ++ j) {
if(a[i].grade < a[j].grade) {
student t = a[i];
a[i] = a[j];
a[j] = t;
}
}
}// 记录以下进步以及退步的情况
for(int i = 1; i <= n; ++ i) {
a[i].now = i;
a[i].dex = a[i].pre - a[i].now;
}// 然后按照原先的顺序又排回去
for(int i = 1; i <= n; ++ i) {
for(int j = i + 1; j <= n; ++ j) {
if(a[i].pre > a[j].pre) {
student t = a[i];
a[i] = a[j];
a[j] = t;
}
}
}
int add = 0, del = 0;// 这里就是直接输出结果了
for(int i = 1; i <= n; ++ i) {
printf("%d ", a[i].dex);
if(a[i].dex > 0) add++;
else if(a[i].dex < 0) del ++;
}
printf("\n%d %d\n", del, add);
}
return 0;
}
A. 简单题
- tag: 高精度,二分
我们已知
b
,
p
b,p
b,p 。我们可以用一个线段表示
a
a
a,那么这个线段上就存在一个点(下图的点
A
A
A)使得
a
b
=
=
p
a^b == p
ab==p(题目已经保证了数据有解),那么这个点的左边就是
a
b
<
p
a^b < p
ab<p,有边为
a
b
>
p
a^b > p
ab>p,也就是下图。我们如何高效的求解图中的点
A
A
A,答案是二分。至于
a
b
a^b
ab会超过任何类型的范围,我们可以采用高精度求解。
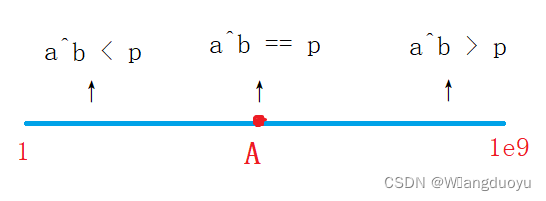
参考代码:
#include <stdio.h>
#include <string.h>
#define ll long long
#define N 1010
ll b, a[N], len;
char p[N];
void init() {
len = 1;
a[0] = 1;
}
void mul(ll b) {
for(ll i = 0; i < len; ++ i) a[i] *= b;
ll cf = 0;
for(ll i = 0, t = 0; i < len; ++ i) {
t = a[i] + cf;
a[i] = t % 10;
cf = t / 10;
}
while(cf) a[len ++] = cf % 10, cf /= 10;
}
void a_b(ll _a, ll _b) {
init();
for(ll i = 0; i < _b; ++ i)
mul(_a);
}
int cmp(ll *a, char *p) {
int lp = strlen(p);
if(len > lp) return 1;
if(len < lp) return -1;
for(int i = len - 1; i >= 0; -- i) {
if(a[i] > p[len - i - 1] - '0') return 1;
else if(a[i] < p[len - i - 1] - '0') return -1;
}
return 1;
}
int main()
{
while(scanf("%lld%s", &b, p) != EOF)
{
// 二分:将区间[l, r] 划分为[l, mid], [mid + 1, r]
ll l = 1, r = 1e9;
while(l < r) {
ll mid = l + r >> 1;
a_b(mid, b);// 求a^b
if(cmp(a, p) == 1) r = mid;
else l = mid + 1;
}
printf("%lld\n", l);
}
}
E. 字符压缩
- tag: C++ STL 字符串问题
定位简单题,不做过多解释。详细请看代码:
#include <bits/stdc++.h>
using namespace std;
string work(string str) //将字符串str解压,并将解压后的结果返回
{
string res = "", word = "";
for(int i = 0; i < str.length(); i ++)
{
if('a' <= str[i] && str[i] <= 'z') word += str[i]; //是字母
else //是数字
{
int number = 0;
int j = i;
while('0' <= str[j] && str[j] <= '9')
{
number = number * 10 + str[j] - '0';
j ++;
}
i = j - 1;
while(number --) res += word; //加上number个word
word = ""; //注意,每次清空word
}
}
return res;
}
int main()
{
string a, b;
cin >> a >> b;
//将a,b解压
a = work(a);
b = work(b);
/*
可以利用string的自带函数find()
下面的a.find(b)就是在a中查找有没有b存在.
如果没有返回string::npos,这个东西一般是-1.
如果找到了就返回b在a中首次出现时其首字符的下标.
*/
if(a == b) puts("A=B");
else if(a.find(b) != -1) puts("A>B");
else if(b.find(a) != -1) puts("A<B");
else puts("A!=B");
return 0;
}
A. 签到题
- tag: 贪心
首先,不要被他吓到了QAQ 然后,我们来分析这道题。我们要将
n
n
n个人分组,分组之后的战斗力为
m
i
n
(
a
1
,
⋅
⋅
⋅
,
a
x
)
∗
x
min(a_1, ···,a_x) * x
min(a1,⋅⋅⋅,ax)∗x 我们要使组数尽可能的多. 那么我们如果使从小到大去分组的话,根据战斗力的计算式,我们会发现只会拖累后面战斗力强的. 所以我们要从大到小 去分组即可 另外,注意此题的数据范围(记得开
l
o
n
g
l
o
n
g
long long
longlong)
参考代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
LL a[N];
bool cmp(LL a, LL b) {
return a > b;
}
int main()
{
int T; cin >> T; // T组数据
while(T -- ) {
int n;
LL m;
cin >> n >> m;
for(int i = 1; i <= n; ++i ) cin >> a[i];
sort(a + 1, a + 1 + n, cmp); // 从大到小排序
LL res = 0, now = 0, cnt = 0;// 分组
for(int i = 1; i <= n; ++ i) {
if(now == 0) now += a[i], ++ cnt;
else {
++ cnt;
now = a[i] * cnt;
}
if(now >= m) ++ res, now = cnt = 0;
}
cout << res << "\n";
}
return 0;
}
D. 解救凡凡
- tag: 模拟
出题人:关于这道题就不得不吐槽一下了,虽然只是想出一个简单模拟,但不小心一改就变难了一diudiu。虽然但是这题和另外几题比起来只是思路需要清晰一点就好,多分析几种情况。看得懂的直接看代码就好。主要注意数据范围,一定要用longlong,考虑清楚五十和五这两个特殊情况,因为100和20和10和2任何一张拆开时最少只用张数加一,但五十和五则需要张数加三,所以在后面需要判定当五或五十存在时,需要判定是否有更优解(能不拆五十和五就不拆),还有就是需要从大的开始拆起,尽量不要拆出更小的面额,所以就需要注意这一点(其实很好满足)注意我样例给的170(就是这个意思),其它细节看代码。主要是考细节,只要够细就能做出来,多if几次就好,题解用了容器,你们用数组也是一样的。
#include<bits/stdc++.h>
using namespace std;
int a[8]={100,50,20,10,5,2,1};
void solve(){
long long n;cin>>n;
long long cnt=0;
vector<long long>ans;
for(int i=0;i<7;i++){
long long x = n/a[i];
cnt+=x;
ans.push_back(x);
n%=a[i];
}
if(cnt&1){
if(ans[4] && ans[6]){//有5有1
ans[4]-=1;
ans[6]-=1;
ans[5]+=3;
cnt+=1;
}
else if(ans[1] && ans[3]){//有50有10
ans[1]-=1;
ans[3]-=1;
ans[2]+=3;
cnt+=1;
}
else if(ans[0]){//100
ans[0]-=1;
ans[1]+=2;
cnt+=1;
}
else if(ans[2]){//20
ans[2]-=1;
ans[3]+=2;
cnt+=1;
}
else if(ans[3]){//10
ans[3]-=1;
ans[4]+=2;
cnt+=1;
}
else if(ans[5]){//2
ans[5]-=1;
ans[6]+=2;
cnt+=1;
}
else if(ans[1]){
ans[1]-=1;
ans[2]+=1;
ans[3]+=3;
cnt+=3;
}
else if(ans[4]){
ans[4]-=1;
ans[5]+=1;
ans[6]+=3;
cnt+=3;
}
}
cout<<cnt;
for(auto e : ans) cout<<" "<<e;
cout<<"\n";
}
int main(){
int t;
cin>>t;
while(t--){
solve();
}
return 0;
}
J. 杨哥哥的acm之路
- tag: 动态规划
如果去掉题意当中" 学习值降为零返回 " 限制的话.
我们考虑dp:
状态表示:
f
[
i
]
[
j
]
f[i][j]
f[i][j]表示从
(
1
,
1
)
(1, 1)
(1,1)->
(
i
,
j
)
(i, j)
(i,j) 的最大学习值
状态计算: 我们发现能到
(
i
,
j
)
(i,j)
(i,j)的只有
(
i
−
1
,
j
)
o
r
(
i
,
j
−
1
)
(i-1,j) or (i, j - 1)
(i−1,j)or(i,j−1) 取上最大值即:
f
[
i
]
[
j
]
+
=
m
a
x
(
f
[
i
−
1
]
[
j
]
,
f
[
i
]
[
j
−
1
]
)
f[i][j] += max(f[i-1][j], f[i][j-1])
f[i][j]+=max(f[i−1][j],f[i][j−1])
我们来看此题的关键, 学习值为零则返回, 那么也就是说只有当前状态学习值为非0的时候才能往下走.我们在dp过程加个判断就好了
参考代码:
#include <bits/stdc++.h>
const int N = 2020;
int dp[N][N], a[N][N];
bool vis[N][N];
void solve()
{
int n, m;
cin >> n >> m;
mem(dp, 0); mem(a, 0); mem(vis, 0); // 初始化
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= m; ++j)
cin >> a[i][j]; // 读入数据
dp[1][1] = a[1][1] + 100; // 起点
if(dp[1][1] <= 0) { // 出师未捷身先死
cout << "NO\n";
return ;
}
vis[1][1] = true; // (1, 1)能往接着走
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= m; ++j)
{ // 如果上一个状态可以接着走的话,那么就可以进行转态转移
if(vis[i - 1][j] && a[i][j] + dp[i - 1][j] > 0)
{
vis[i][j] = true;
dp[i][j] = max(dp[i][j], a[i][j] + dp[i - 1][j]);
}
if(vis[i][j - 1] && a[i][j] + dp[i][j - 1] > 0)
{
vis[i][j] = true;
dp[i][j] = max(dp[i][j], a[i][j] + dp[i][j - 1]);
}
}
if(vis[n][m] && dp[n][m] > 0) // 如果最后为负数也是不行的哦
cout << dp[n][m] << endl;
else
cout << "NO\n";
}
int main() {
int T; cin >> T;
while(T --) solve();
return 0;
}
G. 瓜老板的平方数
- tag: 思维题
如果询问的数本身就是平方数,直接输出 1 1 1。
否则:
如果该数是奇数,设该数为 o d d = 2 x + 1 odd=2x+1 odd=2x+1,
一定有 o d d = ( x + 1 ) 2 − x 2 odd = (x+1)^2-x^2 odd=(x+1)2−x2
如果该数是偶数,设该数为 e v e n even even,那么它起码用 3 3 3个平方数就可以表示,即 先让 e v e n even even减1,变成奇数的情况,然后就有:
e v e n = 1 2 + o d d even=1^2+odd even=12+odd 且 o d d = ( x + 1 ) 2 − x 2 odd=(x+1)^2-x^2 odd=(x+1)2−x2
e v e n = 1 2 + ( x + 1 ) 2 − x 2 even=1^2+(x+1)^2-x^2 even=12+(x+1)2−x2
至于是否可以使用两个平方数表示出来,可以打个表,提前预处理出来所有 可以仅用两个平方数表示出来的数。
时间复杂度
O
(
n
)
O(n)
O(n)
参考代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
int cnt, arr[N];
int ans[N];
int main()
{
//求出所有的平方数,1e6以内有1000个
for(int i = 1; ; i ++)
{
int t = i * i;
if(t > 1000000) break; //大于1e6停止
//将t存入数组
arr[cnt ++] = t;
ans[t] = 1; //标记平方数的ans=1
}
for(int i = 0; i < cnt; i ++)
for(int j = 0; j < cnt; j ++)
{
int t1 = arr[i] + arr[j];
int t2 = arr[i] - arr[j];
//询问的数是[1,1e6]范围内的正整数
if(0 < t1 && t1 <= 1000000 && !ans[t1]) ans[t1] = 2;
if(0 < t2 && t2 <= 1000000 && !ans[t2]) ans[t2] = 2;
}
int q; scanf("%d", &q);
while (q --)
{
int x;
scanf("%d", &x);
if(ans[x]) printf("%d\n", ans[x]); //之前标记过x就直接输出ans[x]
else printf("3\n"); //否则就是3
}
return 0;
}
H. 我也经常单杀他的
- tag: BFS
想法一:
因为我们可以打碎一块墙(也就是1),而我们不知道打碎哪一块才是最优的,直观的想法是去暴力枚举每一个1,求出当该1被打碎的情况下的用时,然后在所有的情况当中取一个最小值。(当然这种做法是会超时的
参考代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 510;
struct Node {int x, y;};
int dx[] = {-1, 1, 0, 0}, dy[] = {0, 0, -1, 1};
int n, m, t;
int tx, ty, fx, fy;
char g[N][N];
int d[N][N];
void bfs()
{
for(int i = 0; i < n; i ++)
for(int j = 0; j < m; j ++) d[i][j] = -1;
queue<Node> q;
q.push({tx, ty}), d[tx][ty] = 0;
while(!q.empty())
{
Node u = q.front();
q.pop();
for(int i = 0; i < 4; i ++)
{
int nx = u.x + dx[i], ny = u.y + dy[i];
if(nx < 0 || nx >= n || ny < 0 || ny >= m || g[nx][ny] == '1') continue;
if(d[nx][ny] != -1) continue;//已经被访问过了
d[nx][ny] = d[u.x][u.y] + 1;
q.push({nx, ny});
}
}
}
int main()
{
scanf("%d%d%d", &n, &m, &t);
for(int i = 0; i < n; i ++) scanf("%s", g[i]);
for(int i = 0; i < n; i ++)
for(int j = 0; j < m; j ++)
{
if(g[i][j] == 'T') tx = i, ty = j, g[i][j] = '0';
if(g[i][j] == 'F') fx = i, fy = j, g[i][j] = '0';
}
bfs();
int ans;
if(d[fx][fy] == -1) ans = 1e8;
else ans = d[fx][fy];
for(int i = 0; i < n; i ++)
for(int j = 0; j < m; j ++)
if(g[i][j] == '1')
{
g[i][j] = '0';
bfs();
g[i][j] = '1';
if(d[fx][fy] != -1) ans = min(ans, d[fx][fy]);
}
if(ans <= t) printf("YES\n%d\n", ans);
else printf("NO\n");
return 0;
}
想法二:
有了上面的思考,我们可以想一想怎么优化,不去暴力枚举每一个墙。
首先,如果T可以通过打碎某一个墙从而到达F,意味着从T开始一定可以遍历到该墙的位置,从F开始也一定可以遍历到该墙的位置。
因此,我们可以仅通过两次bfs来达到目的,第一次以T为起点遍历,并在这个过程中把T所有能到达的1(墙)用其最短距离d1打上标记,第二次以F为起点,并在这个过程中吧F所有能到达的1用其最短距离d2打上标记。
做完这些之后,我们去枚举每一个1的位置,如果它被T和F同时标记上了,意味着T可以通过该位置到达F,并且这个距离就是它们标记的距离之和d1+d2,然后我们在所有的可能中取一个最小值就好了。
参考代码:
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
using namespace std;
typedef long long LL;
const int N = 510;
struct Node {int x, y;};
int dx[] = {-1, 1, 0, 0}, dy[] = {0, 0, -1, 1};
int n, m, t;
int tx, ty, fx, fy;
char g[N][N];
int d1[N][N], d2[N][N];
void bfs(int d[][N], int x, int y)
{
queue<Node> q;
q.push({x, y}), d[x][y] = 0;
while(!q.empty())
{
Node u = q.front();
q.pop();
for(int i = 0; i < 4; i ++)
{
int nx = u.x + dx[i], ny = u.y + dy[i];
if(nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
if(d[nx][ny] != -1) continue;
d[nx][ny] = d[u.x][u.y] + 1;
if(g[nx][ny] != '1') q.push({nx, ny});//不是墙的时候才能加入队列
}
}
}
int main()
{
scanf("%d%d%d", &n, &m, &t);
for(int i = 0; i < n; i ++) scanf("%s", g[i]);
for(int i = 0; i < n; i ++)
for(int j = 0; j < m; j ++)
{
if(g[i][j] == 'T') tx = i, ty = j, g[i][j] = '0';
if(g[i][j] == 'F') fx = i, fy = j, g[i][j] = '0';
}
memset(d1, -1, sizeof d1);
memset(d2, -1, sizeof d2);
bfs(d1, tx, ty);
bfs(d2, fx, fy);
int ans;
if(d1[fx][fy] != -1) ans = d1[fx][fy];
else ans = 1e8;
for(int i = 0; i < n; i ++)
for(int j = 0; j < m; j ++)
{
if(g[i][j] == '1' && d1[i][j] != -1 && d2[i][j] != -1)
{
ans = min(ans, d1[i][j] + d2[i][j]);
}
}
if(ans <= t) printf("YES\n%d\n", ans);
else printf("NO\n");
return 0;
}
