论文

NLP论文笔记合集（持续更新）

原论文：《Attention is All you Need》

最早的提出attention模型的文章：《Neural Machine Translation by Jointly Learning to Align and Translate》

模型结构

整体结构

输入

$\mathbf{x}=(x_1,\dots ,x_n)$，$x$ 为一个中文词，$\mathbf{x}$为中文的一个句子。

输出

$\mathbf{y}=(y_1,\dots ,y_m)$，$y$ 为一个英文词，$\mathbf{x}$为英文的一个句子。

文章部分翻译

3 Model Architecture

极具竞争力的神经序列转录模型都有encoder-decoder结构[5,2,29]。这里，encoder将以symbol表示的 $(x_1,\dots ,x_n)$ 输入序列映射到连续表示 $\mathbf{z}=(z_1,\dots ,z_n)$ 的序列。给定$\mathbf{z}$，然后decoder一次生成symbol表示的输出序列 $(y_1,\dots ,y_m)$的一个元素。在每一步中，模型都是自回归的[9]，在生成下一步时，使用先前生成的symbol作为额外输入。

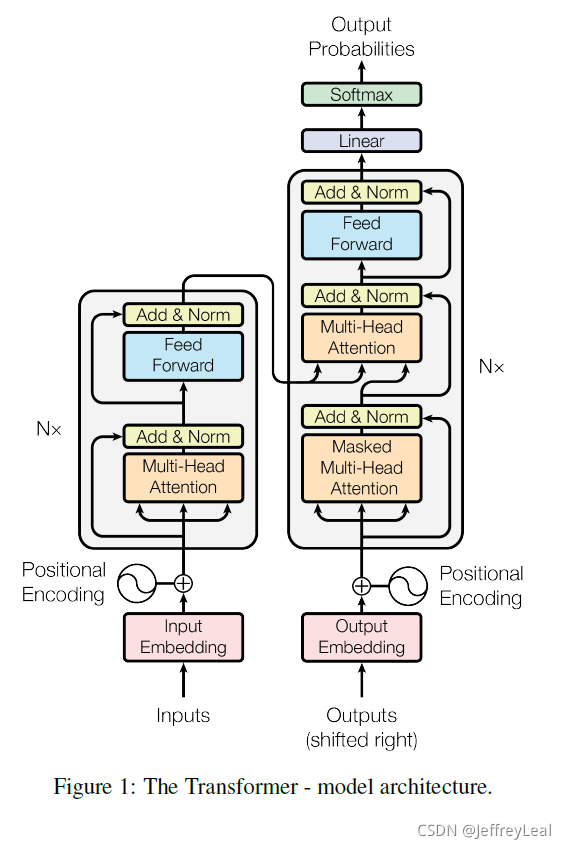
Transformer 遵循这一总体架构，encoder和decoder都使用堆叠的self-attention和逐点全连接层，分别如图1的左半部分和右半部分所示。

3.1 Encoder and Decoder Stacks

$\mathbf{E}\mathbf{n}\mathbf{c}\mathbf{o}\mathbf{d}\mathbf{e}\mathbf{r}$：encoder由N=6个相同层堆叠而成。每层有两个子层。第一个子层是multi-head self-attention结构，第二个子层是简单的、对应位置逐个相乘的全连接前馈网络。我们在两个子层的每个层周围使用residual connection[10]，然后进行layer normalization[1]。也就是说，每个子层的输出是LayerNorm（x+Sublayer（x）），其中Sublayer（x）是由子层本身实现的函数。为了便于residual connection进行连接，模型中的所有子层以及embedding层都会生成尺寸为 $d_{model}=512$ 的输出。

$\mathbf{D}\mathbf{e}\mathbf{c}\mathbf{o}\mathbf{d}\mathbf{e}\mathbf{r}$：decoder也由N=6个相同层的堆栈组成。除了每个encoder层中的两个子层之外，decoder还插入第三个子层，该子层对encoder堆的输出执行multi-head attention。与encoder类似，我们在每个子层周围使用residual connection，然后进行layer normalization。我们还修改了decoder堆栈中的self-attention子层，以防止当前位置关注到未来位置的信息。这种masking，基于输出的embedding偏移一个位置的事实，确保位置 $i$ 的预测只能依赖于位置小于 $i$ 的已知输出。

3.2 Attention

attention函数可以描述为将query和一组key-value对映射到输出的一个映射，其中query、key、value和输出都是向量。输出由value的加权计算得到，其中分配给每个value的权重由query的匹配函数与相应key计算得到。

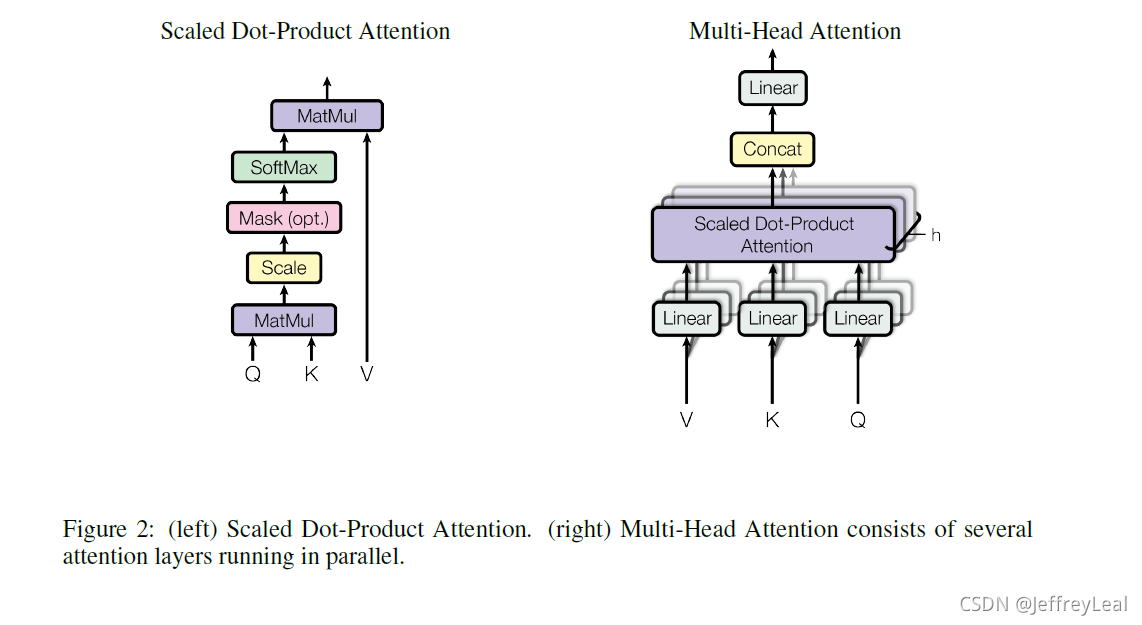
3.2.1 Scaled Dot-Product Attention

我们称我们这个独特的attention为“Scaled Dot-Product Attention”（图2）。输入包括维度 $d_k$ 的query和key以及维度 $d_v$ 的value。我们用所有key计算query的点积，每个除以 $\sqrt{d_k}$，并应用softmax函数以获得value的权重。

在实践中，我们同时计算attention函数，基于一组query，将它们打包成矩阵$Q$。key和value也打包成矩阵$K$和$V$。我们将输出矩阵计算为：
$$Attention(Q,K,V)=softmax(\frac{Q{K}^T}{\sqrt{d_k}})V$$
两种最常用的attention函数是加性attention[2]和点积（多重复制）attention。点积attention与我们的算法相同，只是比例因子$\sqrt{d_k}$不同。加性attention使用带有单个隐藏层的前馈网络计算匹配函数。虽然两者在理论复杂性上相似，但由于可以使用高度优化的矩阵乘法代码来实现，因此在实践中，点积注意速度更快，空间效率更高。

而对于较小的$d_k$值，这两种机制的表现类似，对于较大的$d_k$值，加性attention优于点积attention[3]。我们怀疑，对于较大的$d_k$值，点积的增长幅度较大，从而将softmax函数推到梯度非常小的区域${}^4$。为了抵消这一影响，我们通过给点积乘上$\frac{1}{\sqrt{d_k}}$。

${}^4$为了说明点积变大的原因，假设组成元素$q$和$k$的平均值为0，方差为1的独立随机变量。那么它们的点积$q\cdot k={\sum }_{i=1}^{d_k}{q}_i{k}_i$的均值为0，方差为$d_k$。

3.2.2 Multi-Head Attention

我们发现，不直接使用 $d_{model}$ 维的query、key和value输入到一个attention函数，而是使用不同的经过学习的线性投影矩阵 $h$ 次将query、key和value分别线性投影到 $d_k、d_k$ 和 $d_v$ 维，会更有帮助的。在query、key和value的每个不同投影矩阵上，我们并行执行attention函数，生成 $d_v$ 维输出值。如图2所示，这些值被连接并再次投影，从而得到最终值。

multi-head attention允许模型共同关注来自不同位置的不同表征子空间的信息。平均操作会抑制这种关注能力，只使用一个attention head的话。
$$MultiHead(Q,K,V)=Concat(hea{d}_1,...,hea{d}_h)W^O$$$$wherehea{d}_i=Attention(Q{W}_i^Q,K{W}_i^K,V{W}_i^V)$$
其中投影都是参数矩阵 $W_i^Q\in R^{d_{model}\times d_k},W_i^K\in R^{d_{model}\times d_k},W_i^V\in R^{d_{model}\times d_v}$

在这项工作中，我们采用了$h=8$个平行的attention层或attention head。对于每一个，我们使用$d_k=d_v=d_{model}/h=64$。由于每个头部的维数减小，因此总的计算成本与全维single-head attention的计算成本相似。

3.2.3 Applications of Attention in our Model

Transformer以三种不同的方式使用multi-head attention：

•在“encoder-decoder attention”层中，query来自前一个decoder子层，key和value来自encoder的输出。这允许decoder中的每个位置都关注到输入序列的所有位置。这模仿了sequence-to-sequence模型中典型的encoder-decoder attention机制，如[31,2,8]。

•encoder包含self-attention层。在self-attention层中，所有query、key和value都来自同一个位置，在本例中，是encoder中前一层的输出。encoder中的每个位置都可以关注encoder前一层中的所有位置。

•类似地，decoder中的self-attention层允许decoder中的每个位置关注decoder中直到并包括该位置的所有位置。我们需要防止decoder中的信息向左流动，以保持自回归特性。在scaled dot-product attention中，我们通过mask softmax输入中，所有与非法连接对应的值（设置为 −$\infty$)，来实现这一点 。参见图2。

3.3 Position-wise Feed-Forward Networks

除了attention的子层之外，还有encoder和decoder，他们的每一层都包含一个全连接的前馈网络，该网络分别相同地应用于每个位置。这包括两个线性变换，中间有一个ReLU激活。
$$FFN(x)=\max (0,x{W}_1+b_1)W_2+b_2$$
虽然线性变换在不同位置上是相同的，但它们在层与层之间使用不同的参数。另一种描述方法是将其描述为kernel大小为1的两个卷积。输入和输出的维数为 $d_{model}=512$，内层的维数为 $d_{ff}=2048$。

3.4 Embeddings and Softmax

与其他序列转录模型类似，我们使用学习到的embedding将输入的token和输出的token转换为维度为$d_{model}$的向量。我们还使用常见的学习权重线性变换和softmax函数将decoder输出转换为预测下一个token的概率。在我们的模型中，我们在两个embedding层和预softmax线性变换之间共享相同的权重矩阵，类似于[24]。在embedding层中，我们将这些权重乘以$\sqrt{d_{model}}$。

（注：感觉这里共享是因为，中文和英文的词，意思相同的话，都会在word embedding过程中映射到同一个位置。）

3.5 Positional Encoding

由于我们的模型不包含递归和卷积，为了使模型能够利用序列的顺序，我们必须注入一些关于token在序列中的相对或绝对位置的信息。为此，我们在encoder和decoder堆栈底部的输入embedding中添加“位置编码”。位置编码与embedding具有相同的维度$d_{model}$，因此可以将两者相加。有许多位置编码的选择，学习的和固定的[8]。

在这项工作中，我们使用不同频率的正弦和余弦函数：
$$P{E}_{(pos,2i)}=sin(pos/10000^{2i/d_{model}})$$$$P{E}_{(pos,2i+1)}=cos(pos/10000^{2i/d_{model}})$$
其中$pos$是位置，$i$是维度。也就是说，位置编码的每个维度对应一个正弦曲线。波长形成从 $2\pi$ 到 $10000\cdot 2\pi$ 的几何级数。我们之所以选择这个函数，是因为我们假设它可以让模型通过相对位置轻松学习如何关注信息，因为对于任何固定偏移量 $k$，$P{E}_{pos+k}$可以表示为$P{E}_{pos}$的线性函数。

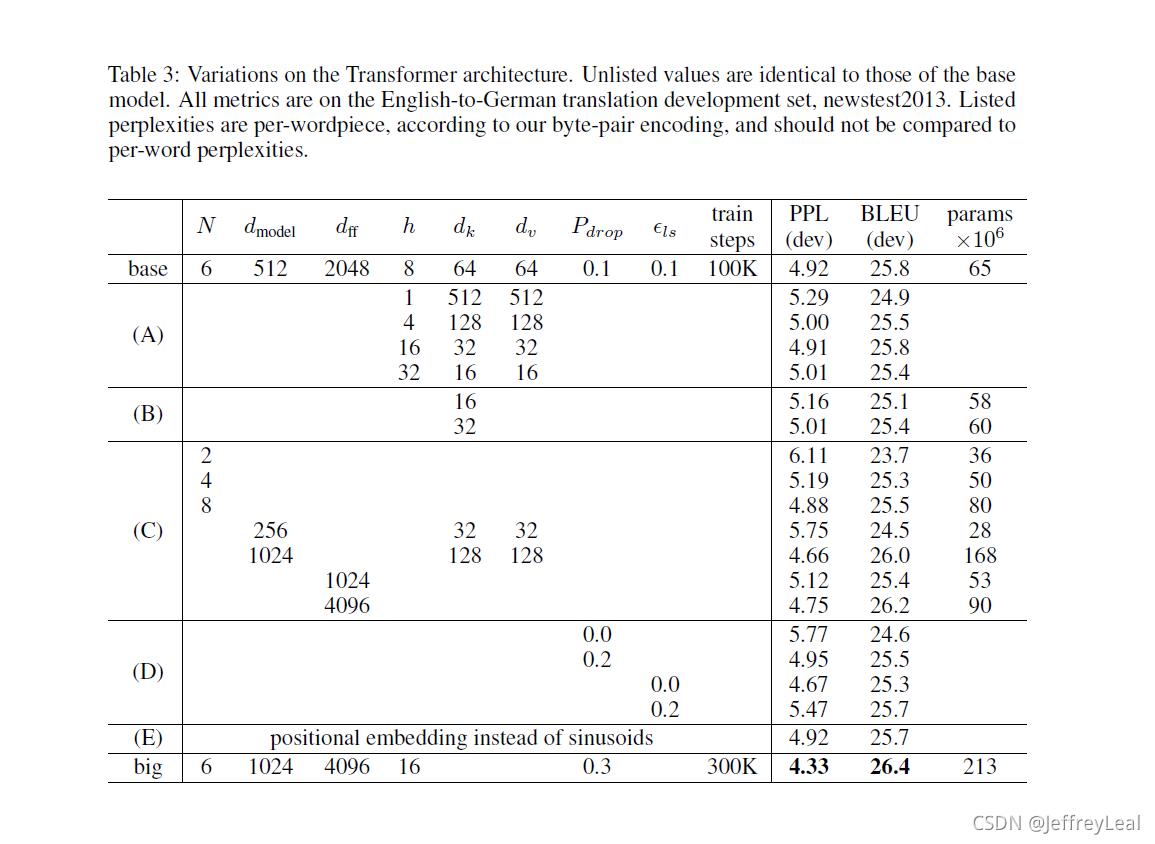
我们还尝试使用习得的位置嵌入[8]，发现这两个版本产生了几乎相同的结果（见表3第（E）行）。我们选择正弦版本，因为它可能允许模型推断出序列长度比训练期间遇到的序列长度更长。

4 Why Self-Attention

相关视频

有的需要科学上网才能看
Transformer论文逐段精读【论文精读】
李宏毅-Transformer
Sequence-to-sequence Learning
【李宏毅】Transformer Seq2seq

相关的笔记

相关代码

pytorch

MorvanZhou /NLP-Tutorials：代码中n代表，即包含batch size；step代表输入句子长度，即一句话包含多少个词；model_dim、dim、emb_dim代表word embedding的维度。

tensorflow

作者的代码

keras

pytorch API:

tensorflow API