学校给的练习题，应该是蓝桥杯的吧，找规律，写，调试代码花了一小时半，菜鸡来发个博客记录一下

题如下：

如图p1.png所示的螺旋折线经过平面上所有整点恰好一次。  

对于整点(X, Y)，我们定义它到原点的距离dis(X, Y)是从原点到(X, Y)的螺旋折线段的长度。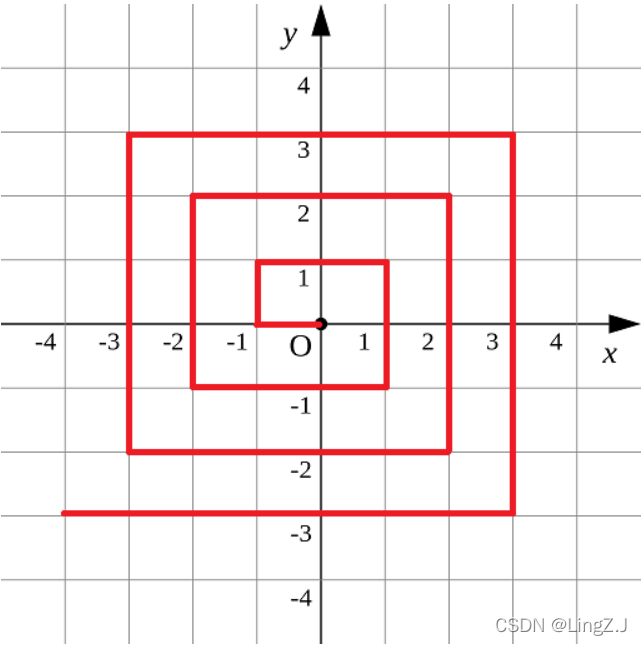  

例如dis(0, 1)=3, dis(-2, -1)=9  

给出整点坐标(X, Y)，你能计算出dis(X, Y)吗？

【输入格式】

X和Y  

对于40%的数据，-1000 <= X, Y <= 1000  

对于70%的数据，-100000 <= X， Y <= 100000  

对于100%的数据, -1000000000 <= X, Y <= 1000000000  

【输出格式】

输出dis(X, Y)  

【样例输入】

0 1

【样例输出】

3

规律如图：

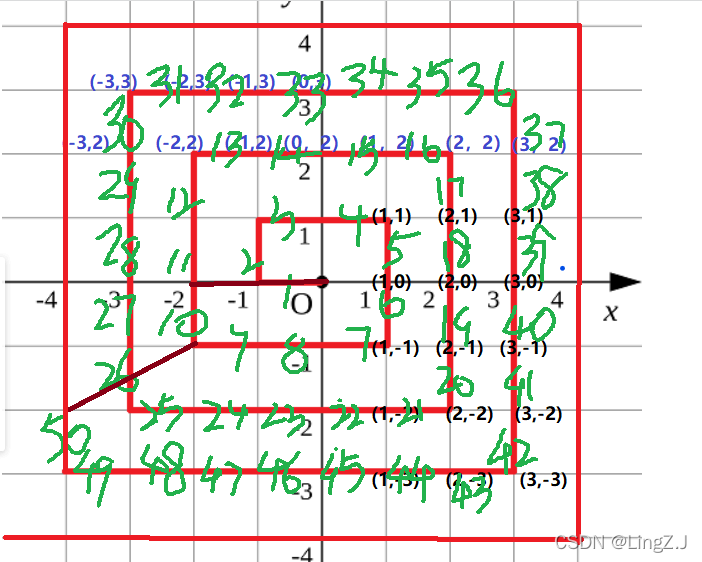
从我数出的边数可以看到，

dis(1,1)=4=(1*2)^2,  dis(2,2)=16=(2*2)^2,  dis(3,3)=36=(2*3)^2

 所以选定一个参考点，这里以每个方形的右上角为例，例如选(3,3)，如果测试点为(-3,0),那么我只需要往回走（3-（-3））+（3-0）步，如果测试点为（2，-3），那么我需要往前走（3-（-3））+（3-2）步

往回走是在参考点的dis的基础上减掉，往前走是在参考点的dis的基础上加上

这里又涉及怎么判断点是往回还是往前

还有一个点需要注意的是，当测试点y的值与参考点一致时，只需要横向往回走减去测试点x与参考点x的距离

代码如下：

public static void main(String[] args) {
        long x,y;
        Scanner sc = new Scanner(System.in);
        x=sc.nextInt();
        y=sc.nextInt();
        //System.out.println(x+" "+y);//调试用的
        getDis(x,y);//传入测试点
    }
    public static void getDis(long x,long y){
        long xx,yy;
        if(x<0)            /*判断x，y是否小于0，若是，取反，这里可以直接-x，-y
                           */
            xx=Math.abs(x);
        else
            xx=x;
        if(y<0)
            yy=Math.abs(y);
        else
            yy=y;
        long max = Math.max(xx,yy);
/*为什么取最大值：
     是为了确定参照点，例如（2，-3）该点应是属于（3，3）这个点的圈的，选x，y绝对值最大
     的那个做判定
*/
        long powdis = 4*max*max;         //其实就是（2*max）^2=dis(max,max)
        //System.out.println(powdis);//调试用的
        long dis,limit=-max+1;
/*怎么判断是往回还是往前：
      仔细观察图可发现，每一圈的起始点其实就位于终点的正上方
      例如参考点（3，3），第三圈终点是（-3，-3），起始点就是（-3，-2）
      所以测试点如果介于起始点和参考点之间，就要往回走；若是过了参考点，就直接往前走
      那么判断往回的条件即是：
           测试点（x，y），参考点（a，b），起始点（-a,-b+1)
           -b+1<=y<b&&-a<=x<a
           （可以包含参考点在内也可以不包含）
*/
        if(y==max)          //判断一下y是否和参考点同在一条水平线上，若是，则只用减掉x的部分
            dis=powdis-(max-x);
        else if(y>=limit&&x<max)
            dis=powdis-(max-x)-(max-y);
        else
            dis=powdis+(max-x)+(max-y);
        System.out.println(dis);
    }

 

 以上就是本人对这道题的拙见，如有疑问或是更好的想法，欢迎在下方评论区留言讨论