7.3.1二叉排序树

代码实现

#pragma once
#include <iostream>
using namespace std;

typedef int KeyType;
typedef int InfoType;
#define ENDFLAG 2021

//二叉排序树的二叉链表存储表示
//结点的数据域类型定义
typedef struct
{
	KeyType key;//关键字项
	InfoType otherinfo;//其他数据项

}ElemType;
//二叉链表
typedef struct BSTNode
{
	ElemType data;//数据域
	struct BSTNode* lchild, * rchild;//左右孩子指针
}BSTNode,*BSTree;


//算法7.5　二叉排序树的插入
void InsertBST(BSTree& T, ElemType e)
{
	//当二叉排序树T中不存在关键字等于e.key的数据元素时，则插入该元素
	if (!T) 
	{									//找到插入位置，递归结束
		BSTNode* S = new BSTNode;         //生成新结点*S
		S->data = e;					//新结点*S的数据域置为e   
		S->lchild = S->rchild = NULL;	//新结点*S作为叶子结点
		T = S;            				//把新结点*S链接到已找到的插入位置
	}
	else if (e.key < T->data.key)
	{
		//将*S插入左子树
		InsertBST(T->lchild, e);			
	}
		
	else if (e.key > T->data.key)
	{
		//将*S插入右子树
		InsertBST(T->rchild, e);			
	}
		
}


//算法7.6　二叉排序树的创建
void CreateBST(BSTree& T)
{
	//依次读入一个关键字为key的结点，将此结点插入二叉排序树T
	T = NULL; //将二叉排序树T初始化为空树
	ElemType e;
	cin >> e.key;
	//ENDFLAG为自定义常量，作为输入结束标志
	while (e.key != ENDFLAG)
	{
		InsertBST(T, e);//将此结点插入二叉排序树T中
		cin >> e.key;
	}

}


//中序遍历二叉树的递归算法
void InOrderTraverse(BSTree T)
{
	//若二叉树非空
	if (T) 
	{
		//中序遍历左子树
		InOrderTraverse(T->lchild);
		//访问根节点
		cout << T->data.key <<" ";
		//中序遍历右子树
		InOrderTraverse(T->rchild);

	}
}


//算法7.4　二叉排序树的递归查找
BSTree SearchBST(BSTree T, KeyType key) 
{
	//在根指针T所指二叉排序树中递归地查找某关键字等于key的数据元素
	//若查找成功，则返回指向该数据元素结点的指针，否则返回空指针
	if ((!T) || key == T->data.key) 
	{
		return T; //查找结束
	}
		
	else if (key < T->data.key)
	{
		return SearchBST(T->lchild, key);//在左子树中继续查找
	}
	else
	{
		return SearchBST(T->rchild, key);//在右子树中继续查找
	}    		   			
}

//算法 7.7　二叉排序树的删除
void DeleteBST(BSTree& T, KeyType key) 
{
	//从二叉排序树T中删除关键字等于key的结点
	//初始化
	BSTNode* p = T; //被删结点
	BSTNode* f = NULL;//双亲结点
	BSTNode* q;
	BSTNode* s;
	/*------------下面的while循环从根开始查找关键字等于key的结点*p-------------*/
	while (p) 
	{
		if (p->data.key == key)
		{
			break;//找到关键字等于key的结点*p，结束循环
		}
		//*f为*p的双亲结点
		f = p;                          
		if (p->data.key > key)
		{
			p = p->lchild;//在*p的左子树中继续查找
		}
		else
		{
			p = p->rchild;//在*p的右子树中继续查找
		}
	}
	//找不到被删结点则返回
	if (!p)
	{
		return;                         		
	}

	/*―考虑三种情况实现p所指子树内部的处理：*p左右子树均不空、无右子树、无左子树―*/
	q = p;
	//被删结点*p左右子树均不空
	if ((p->lchild) && (p->rchild)) 
	{     		
		
		s = p->lchild;
		while (s->rchild)   //在*p的左子树中继续查找其前驱结点，即最右下结点
		{
			q = s; 
			s = s->rchild; //向右到尽头
		}	         		
		p->data = s->data;  //s指向被删结点的“前驱”
		if (q != p) 
		{
			q->rchild = s->lchild;  //重接*q的右子树
		}
		else
		{
			q->lchild = s->lchild;  //重接*q的左子树
		}
		delete s;
		return;
	}
	else if (!p->rchild) //被删结点*p无右子树，只需重接其左子树
	{
		p = p->lchild;
	}
	else if (!p->lchild) //被删结点*p无左子树，只需重接其右子树
	{
		p = p->rchild;
	}
		
	/*――――――――――将p所指的子树挂接到其双亲结点*f相应的位置――――――――*/
	if (!f)
	{
		T = p;//被删结点为根结点
	}                     			
	else if (q == f->lchild)
	{
		 f->lchild = p;	//挂接到*f的左子树位置
	}  
	else
	{
		f->rchild = p;//挂接到*f的右子树位置
	}                		
	delete q;
}





int main()
{
	//创建二叉排序树
	BSTree T;
	cout << "请输入若干字符，用回车区分，以2021结束输入" << endl;
	CreateBST(T);
	cout << "当前有序二叉树中序遍历结果为" << endl;
	InOrderTraverse(T);
	cout << endl;

	//待查找的内容
	KeyType key;
	cout << "请输入待查找关键字：";
	cin >> key;
	BSTree result = SearchBST(T, key);
	if (result)
	{
		cout << "找到关键字：" << key << endl;
	}
	else
	{
		cout << "未找到关键字：" << key << endl;
	}

	//待删除的内容
	cout << "请输入待删除的关键字:";
	cin >> key;
	DeleteBST(T, key);
	cout << "当前有序二叉树中序遍历结果为" << endl;
	InOrderTraverse(T);
	cout << endl;

	system("pause");
	return 0;
}

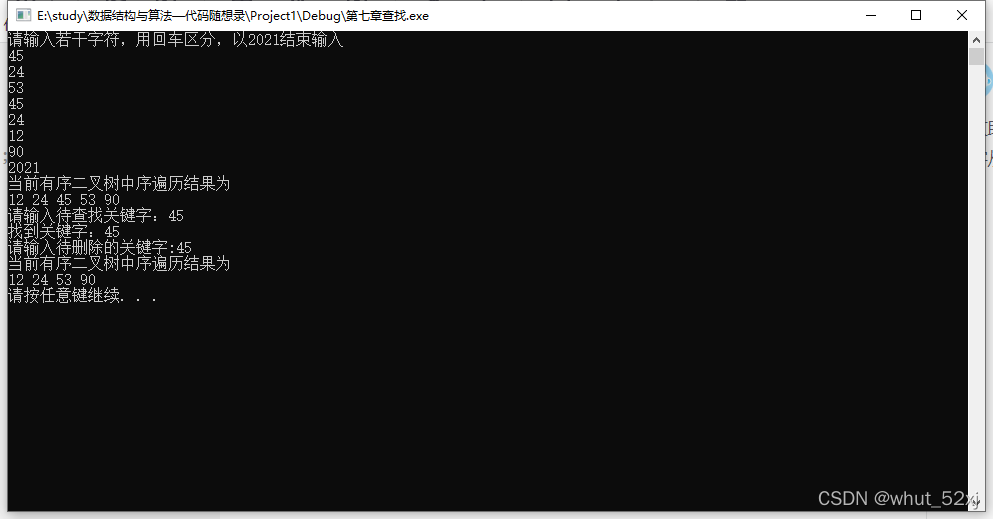
运行结果