目录
十七、LC 60. 排列序列
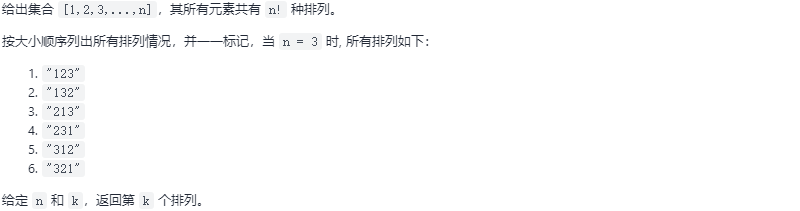
17.1 题求
17.2 求解
十八、LC 22. 括号生成
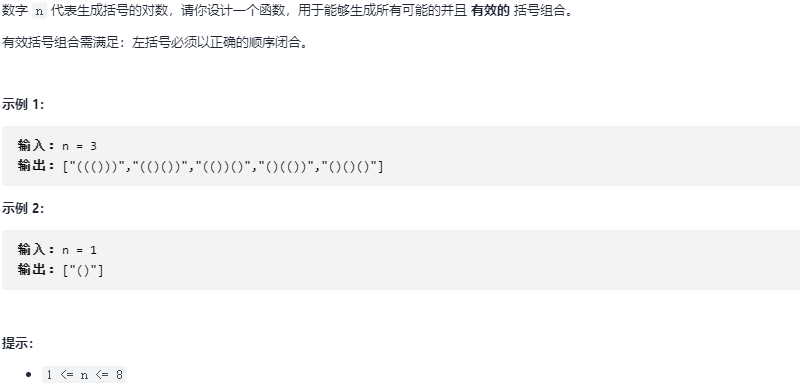
18.1 题求
18.2 求解
十九、LC 753. 破解保险箱
19.1 题求
19.2 求解
十七、LC 60. 排列序列
17.1 题求


17.2 求解
法一:迭代
# 28ms - 94.54%
class Solution:
def getPermutation(self, n: int, k: int) -> str:
from functools import reduce
kinds = reduce(lambda x, y: x*y, range(1, n+1)) # 阶乘 / 当前数组 arr 可构成的不同排列总数
res = [] # 结果列表
arr = [str(i) for i in range(1, n+1)] # 当前可选数字数组 arr
while len(res) < n:
kinds //= len(arr) # 在当前数组 arr 中, 以每个数字开头的不同排列数
idx = (k-1) // kinds # arr 的所有排列中, 第 idx 个数字即为第 k 大排列的首位数字
res.append(arr.pop(idx)) # 将第 idx 个数字移出 arr 并加入结果列表
k -= (idx + 1) * kinds # 更新/对齐 k, 令下一个首位数字在剩余 arr 的所有排列中为第 k 大
return ''.join(res)参考资料:
力扣
十八、LC 22. 括号生成
18.1 题求
18.2 求解
法一:回溯
# 84ms - 6.92%
class Solution:
def generateParenthesis(self, n: int) -> List[str]:
# 设 n=3 种, 则首个必然是 "(" , 末尾必是 ")" 于是剩余左半边只可能有 "((", "()", ")(", "))"
# 显然 "))" 非法, 故可能的左半边只有 "(((", "(()", "()(" 开始回溯并记录所有有效组合
res = []
num = n * 2
choice = {'(', ')'}
def check(arr):
flag = 0
for i in arr:
flag += 1 if i == '(' else -1
# ')' 不可以在任何时候比 '(' 多
if flag < 0:
return False
# '('也不可以比 ')' 多
return flag == 0
def recur(arr):
# 检查
if len(arr) == num:
if check(arr):
res.append(''.join(arr))
return
# 回溯
for j in choice:
arr.append(j)
recur(arr)
arr.pop()
recur(['('])
return res法一改:回溯 + 剪枝 + 有效性检查函数
# 40ms - 38.81%
class Solution:
def generateParenthesis(self, n: int) -> List[str]:
if n == 1:
return ["()"]
res = []
num = n * 2 - 1 # 总数 - 1
choice = {'(', ')'}
def check(arr, half=False):
flag = 0
for i in arr:
flag += 1 if i == '(' else -1
# ')' 不可以在任何时候比 '(' 多
if flag < 0:
return False
# '('也不可以比 ')' 多
return True if half else flag == 0
def recur(arr):
# 半路检查 - 半数时必须满足 num('(') >= num(')') - 相当于剪枝
if len(arr) == n:
if not check(arr, half=True):
return
# 完整检查
elif len(arr) == num:
arr.append(')') # 强制约束最后必为 ')' - 相当于剪枝
if check(arr):
res.append(''.join(arr))
arr.pop() # 及时弹出避免影响后续回溯 (Python list 是 mutable 的)
return
# 回溯
for j in choice:
arr.append(j)
recur(arr)
arr.pop() # 及时弹出避免影响后续回溯 (Python list 是 mutable 的)
# 强制约束首个必为 ')' - 相当于剪枝
recur(['('])
return res法一再改:回溯 + 剪枝 + 有效性计数器 (取代检查函数)
# 36ms - 59.80%
class Solution:
def generateParenthesis(self, n: int) -> List[str]:
res = []
num = n * 2 - 1 # 总数 - 1
choice = {('(', 1), (')', -1)} # type, score
def recur(arr, cnt):
# 任何时候总有 num('(') >= num(')') - 相当于剪枝
if cnt < 0:
return
# 完整检查
if len(arr) == num:
arr.append(')') # 强制约束最后必为 ')' - 相当于剪枝
if cnt == 1:
res.append(''.join(arr))
arr.pop() # 及时弹出避免影响后续回溯 (Python list 是 mutable 的)
return
# 回溯
for j, k in choice:
arr.append(j)
recur(arr, cnt+k)
arr.pop() # 及时弹出避免影响后续回溯 (Python list 是 mutable 的)
recur(['('], 1) # 强制约束首个必为 ')' - 相当于剪枝
return res官方说明

# 128ms - 5.04%
class Solution:
def generateParenthesis(self, n: int) -> List[str]:
def generate(A):
if len(A) == 2*n:
if valid(A):
ans.append("".join(A))
else:
A.append('(')
generate(A)
A.pop()
A.append(')')
generate(A)
A.pop()
def valid(A):
bal = 0
for c in A:
if c == '(':
bal += 1
else:
bal -= 1
if bal < 0:
return False
return bal == 0
ans = []
generate([])
return ans
# 40ms - 38.81%
class Solution:
def generateParenthesis(self, n: int) -> List[str]:
ans = []
def backtrack(S, left, right):
if len(S) == 2 * n:
ans.append(''.join(S))
return
if left < n:
S.append('(')
backtrack(S, left+1, right)
S.pop()
if right < left:
S.append(')')
backtrack(S, left, right+1)
S.pop()
backtrack([], 0, 0)
return ans

# 20ms - 99.76% - 自底向上递归
class Solution:
@lru_cache(None)
def generateParenthesis(self, n: int) -> List[str]:
if n == 0:
return ['']
res = []
for p in range(n):
for left in self.generateParenthesis(p):
for right in self.generateParenthesis(n-1-p):
res.append(f'({left}){right}')
# n 组括号的所有组合
return res
动态规划
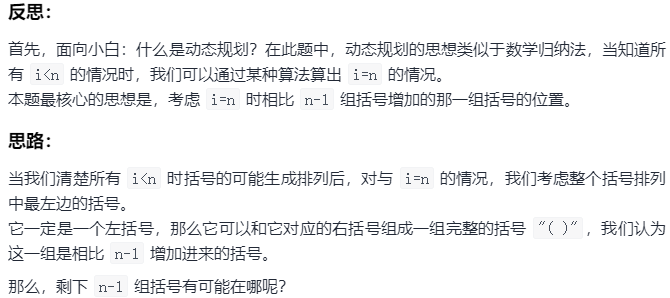

# 24ms - 98.28%
class Solution:
def generateParenthesis(self, n: int) -> List[str]:
# dp[i] 表示 i 组括号的所有有效组合
# dp[i] = "(dp[p] 的所有有效组合)+【dp[q]的组合】"
# 其中 p 从 0 遍历到 i-1, 同时 q 则相应从 i-1 到 0, 始终满足 p+q = i-1
dp = [[] for _ in range(n+1)] # dp[i] 存放 i 组括号的所有有效组合
dp[0].append("") # 初始化 dp[0], 共有 0 组括号时没有组合
dp[1].append("()") # 初始化 dp[1], 共有 0 组括号时组合唯一
# 计算 dp[i], 即共有 i 组括号时的所有组合, 从第 2 组开始
for i in range(2, n+1):
for p in range(i): # 遍历 p, 范围 [0, i]
lst1 = dp[p] # 得到 dp[p] 的所有有效组合
lst2 = dp[i-1-p] # 得到 dp[q] = dp[(i-1)-p] 的所有有效组合
# 遍历各组合插入到当前1组 () 的中、右侧
for k1 in lst1:
for k2 in lst2:
# "(" + 【i=p时所有括号的排列组合】+ ")" +【i=q时所有括号的排列组合】
# p+q = n-1, 即除了 () 外剩下的 n-1 组
dp[i].append(f"({k1}){k2}") # 各 n 组合 "(" + k1+ ")" + k2
return dp[n]参考资料:
力扣
力扣
力扣
十九、</> 数组组成最大数
19.1 题求

19.2 求解
法一:自定义列表排序比较规则
# 12ms - 100%
from functools import cmp_to_key
# functools 中的 cmp_to_key 可将一个 cmp 函数变成一个 key 函数, 从而支持自定义排序
def compare(x, y):
# 当 x > y 时返回 1, x = y 时返回 0, 否则返回 -1
# 它在 list 中的工作机制即对元素两两比较, cmp 返回正数时交换两元素
return int(y+x) - int(x+y)
arr = input()[1:-1].split(',')
arr = sorted(arr, key=cmp_to_key(compare))
print(''.join(arr))# 12ms - 100%
from functools import cmp_to_key
# functools 中的 cmp_to_key 可将一个 cmp 函数变成一个 key 函数, 从而支持自定义排序
arr = input()[1:-1].split(',')
arr.sort(key = cmp_to_key(lambda x, y: int(y+x) - int(x+y)))
print(''.join(arr))网友实现
# 12ms - 100.00%
class myStr(str):
def __init__(self, s):
self.data = s
def __lt__(self, s):
return self.data + s < s + self.data
def comb():
line = input().strip()[1:-1].split(',')
arr = map(myStr, line)
res = sorted(arr, reverse=True)
return "".join(res)
if __name__ == "__main__":
print(comb())参考资料:
力扣
