机器学习1一元线性回归
- 前言
- 一、回归概念
- 高尔顿(达尔文表兄)提出
- 二、线性回归适用场景
- 三、线性回归方程
- 一元线性回归
- 多元线性回归方程
- 拟合直线的原则
- 梯度下降算法
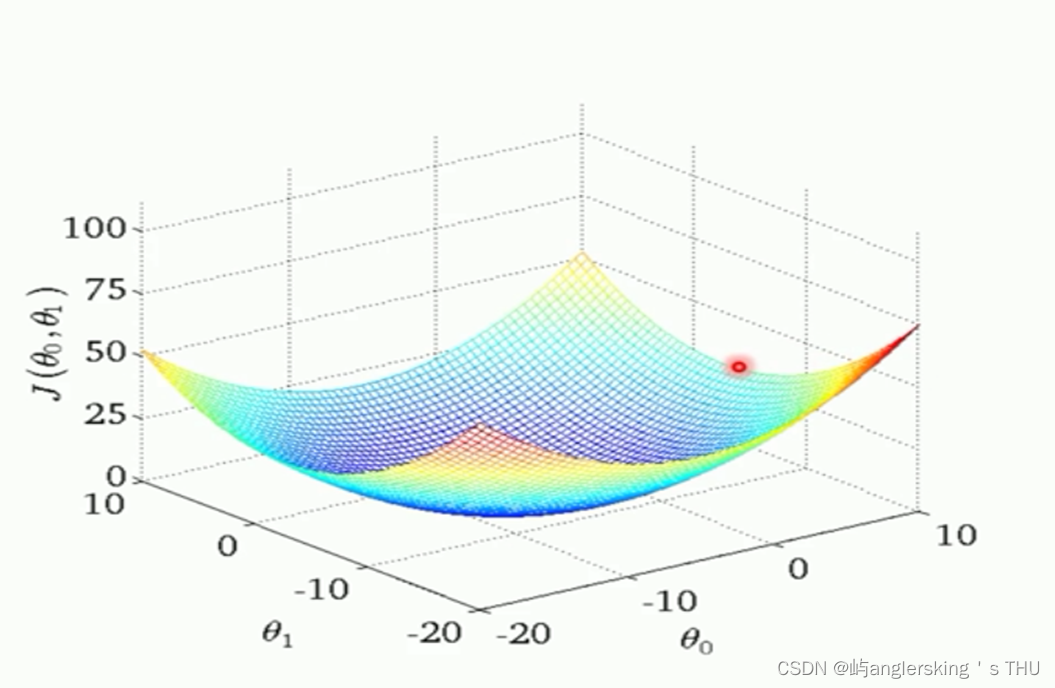
- 凸函数和非凸函数
- 梯度下降学习率
- 例如
- 代价函数
- 一元函数梯度下降
- 上代码实战(房价预测)
前言
本人是技术控所以先从应用开始,最后再进入科普机器学习历史环节
提示:以下是本篇文章正文内容,下面案例可供参考
一、回归概念
高尔顿(达尔文表兄)提出
- 研究父辈身高和字辈身高关系
- 通过大量统计表明矮个子的父辈的子女平均身高高于父辈,高个子身高的父辈子女平均身高低于父辈。
- 通俗的讲,姚明的孩子身高超过姚明的概率很低,潘长江的孩子超过潘长江的概率很高。
- 大自然有种力量让物种趋于平均。这种现象就叫回归
二、线性回归适用场景
- 身高体重预测
- 房价预测
- 等等
三、线性回归方程
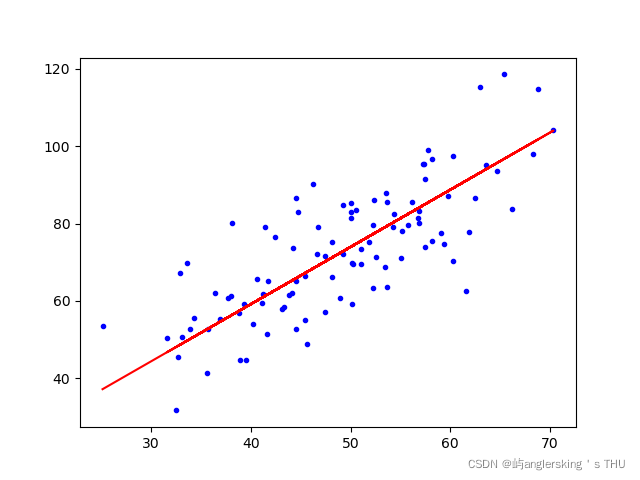
一元线性回归
- f(x) = w1*x+w0
多元线性回归方程
- f(x1,x2…xn) = w0+w1X1+w2X2+…wn*Xn
代码如下(示例):
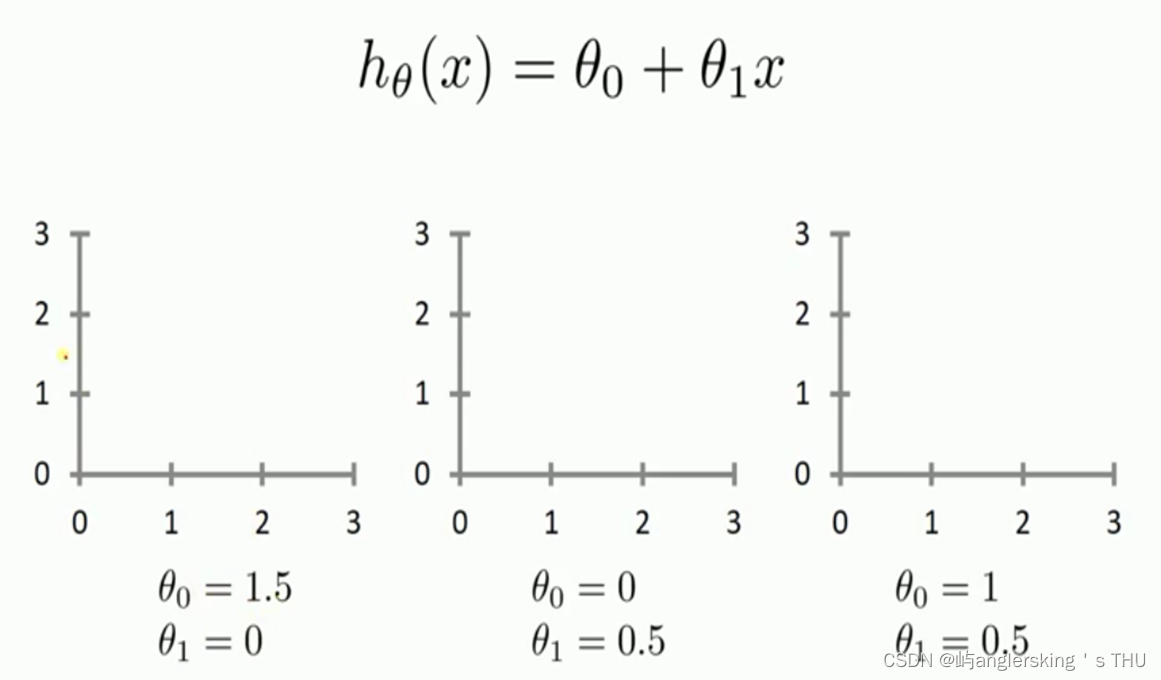
拟合直线的原则
- 最小二乘法
数学必备知识
导数概念
复合函数求导法则
偏导数
极大值,极小值概念
梯度概念



- 真实值和预测值的误差最小
- 每个点和直线的距离平方和最小
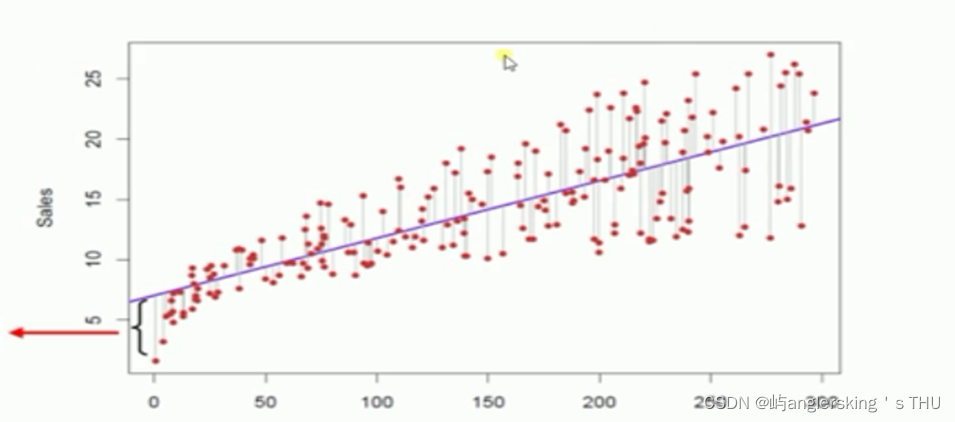
梯度下降算法

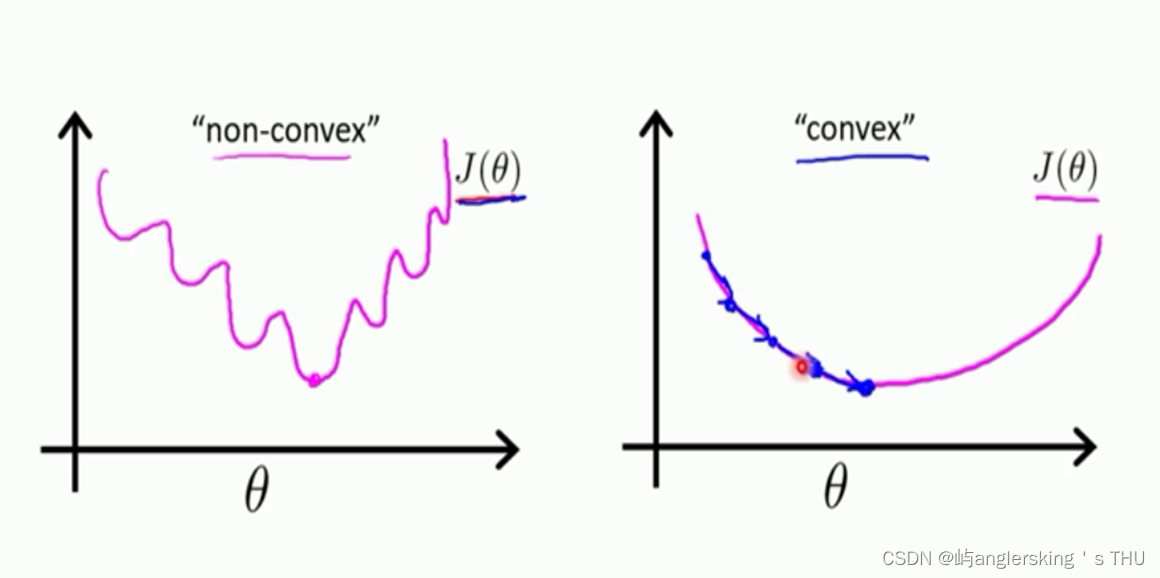
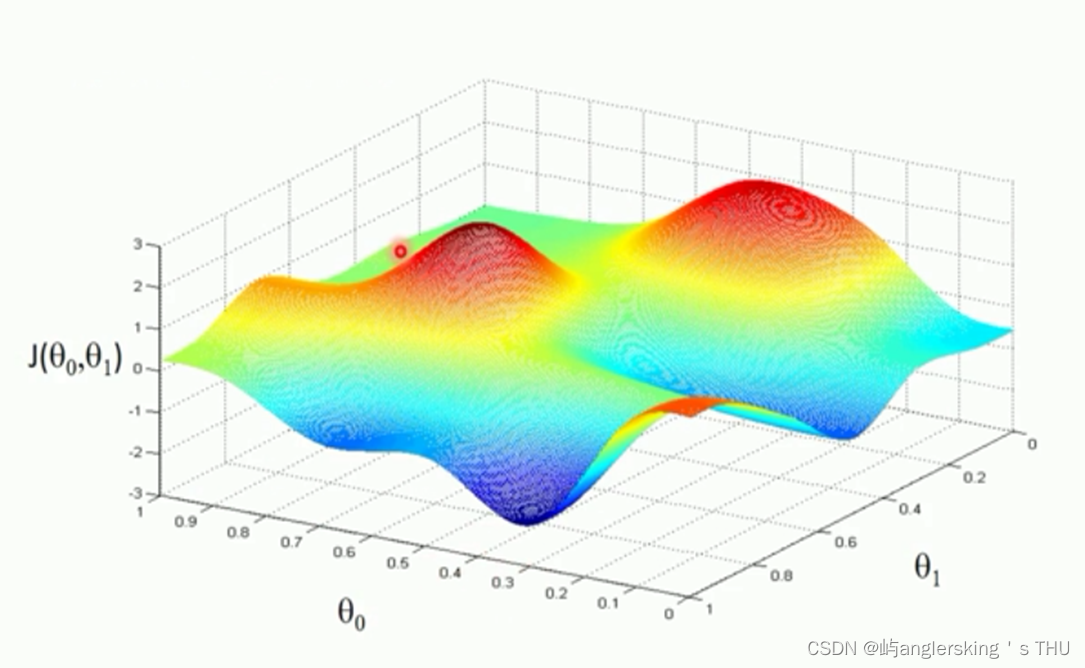
凸函数和非凸函数
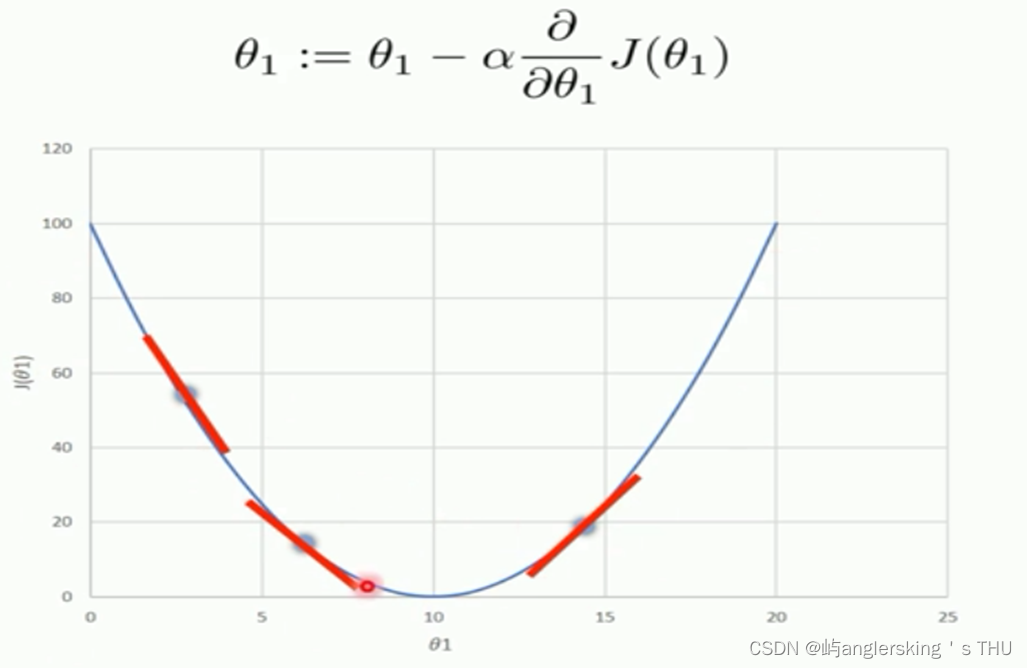
梯度下降学习率
梯度下降算法中被称作为学习率或者步长,意味着我们可以通过α来控制每一步走的距离
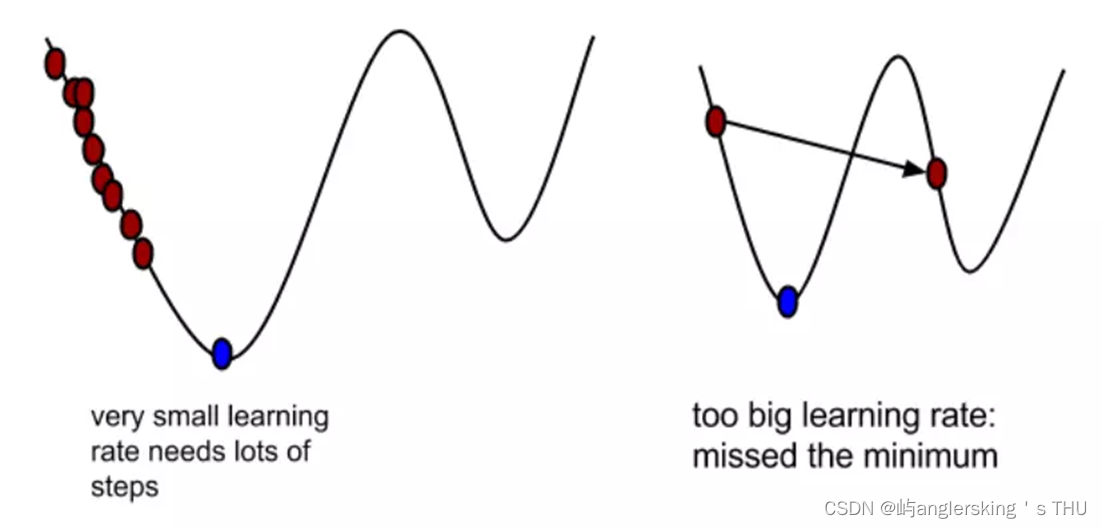
例如


代价函数
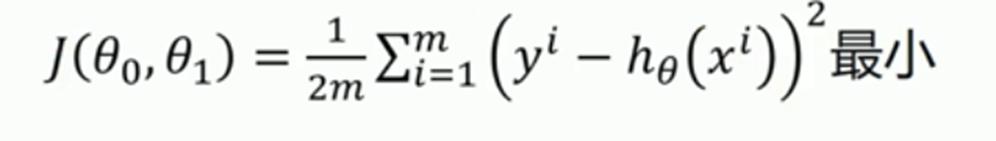
一元函数梯度下降
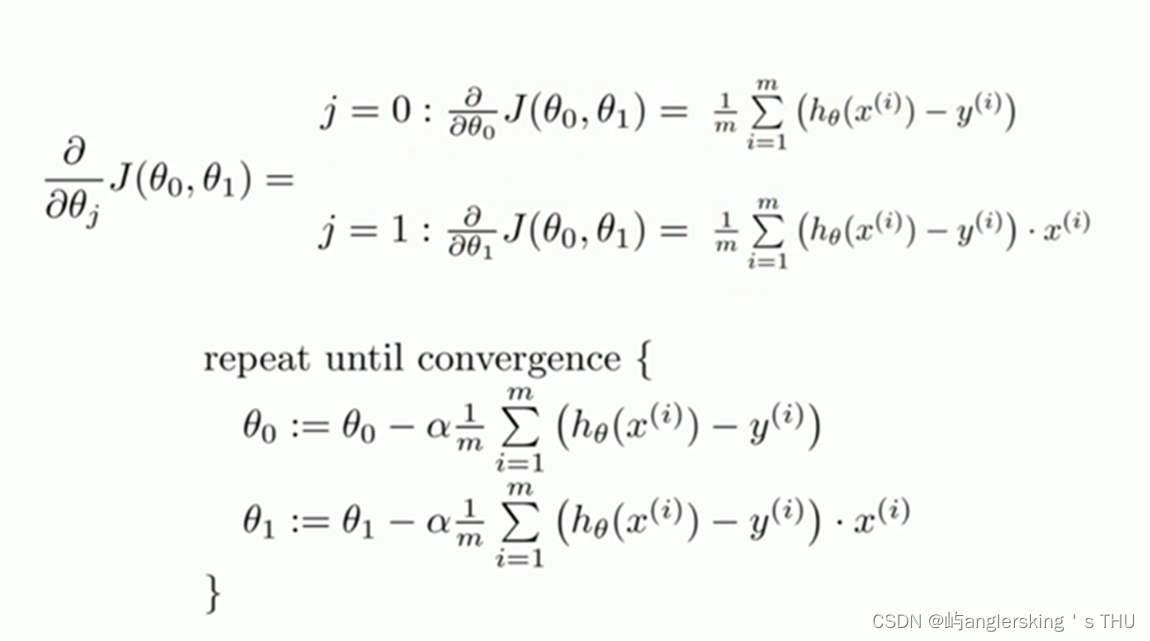
上代码实战(房价预测)
import numpy as np
import matplotlib.pyplot as plt
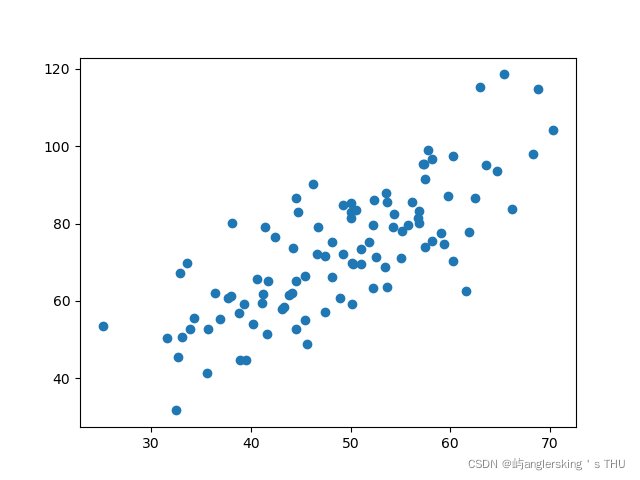
data = np.genfromtxt('data.csv',delimiter=',')
x_data = data[:,0]
y_data = data[:,1]
plt.scatter(x_data,y_data)
plt.show()
w = 0
b = 0
alf = 0.0001
counter = 100
def costFunc(w,b,x_data,y_data):
totErr = 0;
for i in range(len(x_data)):
totErr += (y_data[i]-(w*x_data[i]+b))**2
return totErr/float(len(x_data))
def gradient_decent(x_data,y_data,w,b,alf,counter):
m = float(len(x_data))
for i in range(counter):
w_temp = 0
b_temp = 0
for j in range(len(x_data)):
w_temp += (1/m) * (w*x_data[j]+b-y_data[j])*x_data[j]
b_temp += (1/m) * (w*x_data[j]+b-y_data[j])
w = w-alf*w_temp
b = b-alf*b_temp
if i%5==0:
print("count=",i)
plt.plot(x_data,y_data,'b.')
plt.plot(x_data,w*x_data+b,'r')
plt.show()
print('b={},w={},costErr={}'.format(b,w,costFunc(w,b,x_data,y_data)))
return w,b
w,b = gradient_decent(x_data,y_data,w,b,alf,counter)
100次之后