一、房屋数据集“house_prices.csv”的多元线性回归

1.基础包与数据导入
依次运行如下代码

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

df = pd .read_csv('house_prices.csv')
df.info(); df.head()

输出：

2.数据清洗
1）数据清洗常用方法
1、数字异常值方法
数字异常值方法是一维特征空间中最简单的非参数异常值检测方法，异常值是通过IQR（InterQuartile Range）计算得的。计算第一和第三四分位数（Q1、Q3），异常值是位于四分位数范围之外的数据点x i：使用四分位数乘数值k=1.5，范围限制是典型的上下晶须的盒子图。这种技术是使用KNIME Analytics Platform内置的工作流程中的Numeric Outliers节点实现的。
2、Z-score
Z-score是一维或低维特征空间中的参数异常检测方法。该技术假定数据是高斯分布，异常值是分布尾部的数据点，因此远离数据的平均值。距离的远近取决于使用公式计算的归一化数据点z i的设定阈值Zthr：其中xi是一个数据点，μ是所有点xi的平均值，δ是所有点xi的标准偏差。然后经过标准化处理后，异常值也进行标准化处理，其绝对值大于Zthr。Zthr值一般设置为2.5、3.0和3.5。该技术是使用KNIME工作流中的行过滤器节点实现的。
2）函数实现

# 异常值处理
# ================ 异常值检验函数：iqr & z分数 两种方法 =========================
def outlier_test(data, column, method=None, z=2):
""" 以某列为依据，使用 上下截断点法 检测异常值(索引) """
"""
full_data: 完整数据
column: full_data 中的指定行，格式 'x' 带引号
return 可选; outlier: 异常值数据框
upper: 上截断点; lower: 下截断点
method：检验异常值的方法（可选, 默认的 None 为上下截断点法），
选 Z 方法时，Z 默认为 2
"""
# ================== 上下截断点法检验异常值 ==============================
if method == None:
print(f'以 {column} 列为依据，使用 上下截断点法(iqr) 检测异常值...')
print('=' * 70)
# 四分位点；这里调用函数会存在异常
column_iqr = np.quantile(data[column], 0.75) - np.quantile(data[column], 0.25)
# 1，3 分位数
(q1, q3) = np.quantile(data[column], 0.25), np.quantile(data[column], 0.75)
# 计算上下截断点
upper, lower = (q3 + 1.5 * column_iqr), (q1 - 1.5 * column_iqr)
# 检测异常值
outlier = data[(data[column] <= lower) | (data[column] >= upper)]
print(f'第一分位数: {q1}, 第三分位数：{q3}, 四分位极差：{column_iqr}')
print(f"上截断点：{upper}, 下截断点：{lower}")
return outlier, upper, lower
# ===================== Z 分数检验异常值 ==========================
if method == 'z':
""" 以某列为依据，传入数据与希望分段的 z 分数点，返回异常值索引与所在数据框 """
"""
params
data: 完整数据
column: 指定的检测列
z: Z分位数, 默认为2，根据 z分数-正态曲线表，可知取左右两端的 2%，
根据您 z 分数的正负设置。也可以任意更改，知道任意顶端百分比的数据集合
"""
print(f'以 {column} 列为依据，使用 Z 分数法，z 分位数取 {z} 来检测异常值...')
print('=' * 70)
# 计算两个 Z 分数的数值点
mean, std = np.mean(data[column]), np.std(data[column])
upper, lower = (mean + z * std), (mean - z * std)
print(f"取 {z} 个 Z分数：大于 {upper} 或小于 {lower} 的即可被视为异常值。")
print('=' * 70)
# 检测异常值
outlier = data[(data[column] <= lower) | (data[column] >= upper)]
return outlier, upper, lower

3）Z方法数据清洗

outlier, upper, lower = outlier_test(data=df, column='price', method='z')
outlier.info(); outlier.sample(5)

4）简单丢弃数据

df.drop(index=outlier.index, inplace=True)

3.数据分析
1）热力图

# 热力图 
def heatmap(data, method='pearson', camp='RdYlGn', figsize=(10 ,8)):
    """
    data: 整份数据
    method：默认为 pearson 系数
    camp：默认为：RdYlGn-红黄蓝；YlGnBu-黄绿蓝；Blues/Greens 也是不错的选择
    figsize: 默认为 10，8
    """
    ## 消除斜对角颜色重复的色块
    #     mask = np.zeros_like(df2.corr())
    #     mask[np.tril_indices_from(mask)] = True
    plt.figure(figsize=figsize, dpi= 80)
    sns.heatmap(data.corr(method=method), \
                xticklabels=data.corr(method=method).columns, \
                yticklabels=data.corr(method=method).columns, cmap=camp, \
                center=0, annot=True)
    # 要想实现只是留下对角线一半的效果，括号内的参数可以加上 mask=mask

## 从线性回归结果中提取方差分析结果
import statsmodels.api as sm
from statsmodels.formula.api import ols # ols 为建立线性回归模型的统计学库
from statsmodels.stats.anova import anova_lm

# 数据集样本数量：6028，这里随机选择 600 条，如果希望分层抽样，可参考文章：
df = df.copy().sample(600)

# C 表示告诉 Python 这是分类变量，否则 Python 会当成连续变量使用
## 这里直接使用方差分析对所有分类变量进行检验
## 下面几行代码便是使用统计学库进行方差分析的标准姿势
lm = ols('price ~ C(neighborhood) + C(style)', data=df).fit()
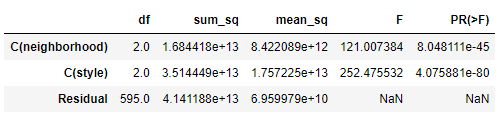
anova_lm(lm)

# Residual 行表示模型不能解释的组内的，其他的是能解释的组间的
# df: 自由度（n-1）- 分类变量中的类别个数减1
# sum_sq: 总平方和（SSM），residual行的 sum_eq: SSE
# mean_sq: msm, residual行的 mean_sq: mse
# F：F 统计量，查看卡方分布表即可
# PR(>F): P 值

# 反复刷新几次，发现都很显著，所以这两个变量也挺值得放入模型中

输出

4.多元线性回归建模
1）建模；

from statsmodels.formula.api import ols

lm = ols('price ~ area + bedrooms + bathrooms', data=df).fit()
lm.summary()

4.模型优化
1）提升模型精度

# 设置虚拟变量
# 以名义变量 neighborhood 街区为例
nominal_data = df['neighborhood']

# 设置虚拟变量
dummies = pd.get_dummies(nominal_data)
dummies.sample()  # pandas 会自动帮你命名

# 每个名义变量生成的虚拟变量中，需要各丢弃一个，这里以丢弃C为例
dummies.drop(columns=['C'], inplace=True)
dummies.sample()

# 将结果与原数据集拼接
results = pd.concat(objs=[df, dummies], axis='columns')  # 按照列来合并
results.sample(3)
# 对名义变量 style 的处理可自行尝试

2）再次建模

# 再次建模
lm = ols('price ~ area + bedrooms + bathrooms + A + B', data=results).fit()
lm.summary()

3）处理多元共线性

# 自定义方差膨胀因子的检测公式
def vif(df, col_i):
    """
    df: 整份数据
    col_i：被检测的列名
    """
    cols = list(df.columns)
    cols.remove(col_i)
    cols_noti = cols
    formula = col_i + '~' + '+'.join(cols_noti)
    r2 = ols(formula, df).fit().rsquared
    return 1. / (1. - r2)

test_data = results[['area', 'bedrooms', 'bathrooms', 'A', 'B']]
for i in test_data.columns:
    print(i, '\t', vif(df=test_data, col_i=i))
# 发现 bedrooms 和 bathrooms 存在强相关性，可能这两个变量是解释同一个问题

lm = ols(formula='price ~ area + bathrooms + A + B', data=results).fit()
lm.summary()

4）多元共线性检查

# 再次进行多元共线性检测
test_data = df[['area', 'bathrooms']]
for i in test_data.columns:
    print(i, '\t', vif(df=test_data, col_i=i))

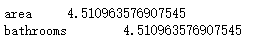
二、Excel重做多元线性回归，求解回归方程

1.导入数据分析

勾选分析工具库

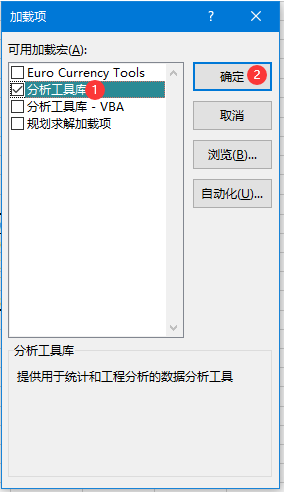
在数据栏中选择数据分析

选择回归

设置回归参数

三、机器学习库Sklearn库多元线性回归

1.导入数据分析
1)导入库

import numpy as np
import pandas as pd
import math
import matplotlib.pyplot as plt
from sklearn import linear_model 
from mpl_toolkits.mplot3d import Axes3D  # 不要去掉这个import
from sklearn.metrics import mean_squared_error, r2_score
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

2）导入数据

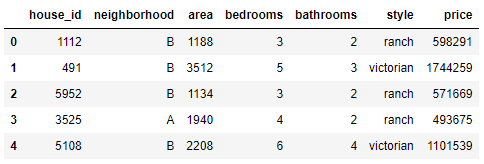
data = pd.read_csv('house_prices.csv')
data.head()

3）去掉无关数据房屋id

new_data=data.iloc[:,1:]
new_data.head()

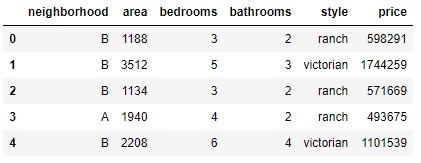
4）分析相关性
通过相关系数矩阵

new_data.corr()

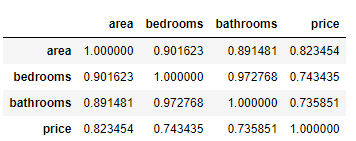
5）线性回归参数设置

x_data = new_data.iloc[:, 1:4] #area、bedrooms、bathroom对应列
y_data = new_data.iloc[:, -1] #price对应列
print(x_data, y_data, len(x_data))

6）回归分析

model = linear_model.LinearRegression()
model.fit(x_data, y_data)
print("回归系数：", model.coef_)
print("截距：", model.intercept_)
print('回归方程: price=',model.coef_[0],'*area +',model.coef_[1],'*bedrooms +',model.coef_[2],'*bathromms +',model.intercept_)

结果

2.对比分析
第一种采用统计分析库statsmodels,对数据进行了清洗，获得的结果更加精确
第二种方法为使用Excel的数据分析工具进行分析
第三种则是采用机器学习sklearn库进行多元回归分析