题目描述

写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项（即 F(N)）。斐波那契数列的定义如下：

F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

示例 1：

输入：n = 2
输出：1
示例 2：

输入：n = 5
输出：5

提示：

0 <= n <= 100

解答思路

正常递归会超时，所以需要使用数学计算方法

快速幂
f(0)=0
f(1)=1

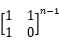
最后输出结果的左上角即可

提交结果

package main

import "fmt"

func main() {
    fmt.Println(fib(0))
    fmt.Println(fib(1))
    fmt.Println(fib(2))
    fmt.Println(fib(3))
    fmt.Println(fib(4))
    fmt.Println(fib(5))
}

func fib(n int) int {
    num := []int{0, 1}
    m := [][]int{{0, 1}, {1, 1}}
    if n == 0 {
        return 0
    } else if n == 1 {
        return 1
    } else {
        for x := n - 2; x >= 0; x-- {
            n1 := num[0]
            n2 := num[1]
            num[0] = (n1*m[0][0] + n2*m[1][0]) % 1000000007
            num[1] = (n1*m[0][1] + n2*m[1][1]) % 1000000007
        }
        return num[1]
    }
    return 0
}

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/fei-bo-na-qi-shu-lie-lcof
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。