支持向量机SVM（分类器）

方法描述

核心思想：

• 本篇中主要以二分类问题为例讨论SVM分类器

• 对于d维样本集，每个样本视作d维空间中的一个点

• 就二分类问题而言：

  • 若样本线性可分，则一定可以找到一个超平面$(W,b)$将d维样本空间分为两个部分，每类样本分别在超平面一边
  • 若样本线性不可分，通过核方法映射到可以线性分开样本的高维，再使用线性分类器

• 对于线性可分数据来说，分割平面不唯一，为了得到唯一确定且最优的分割平面，引入间隔概念（衡量平面两端样本到平面的距离）

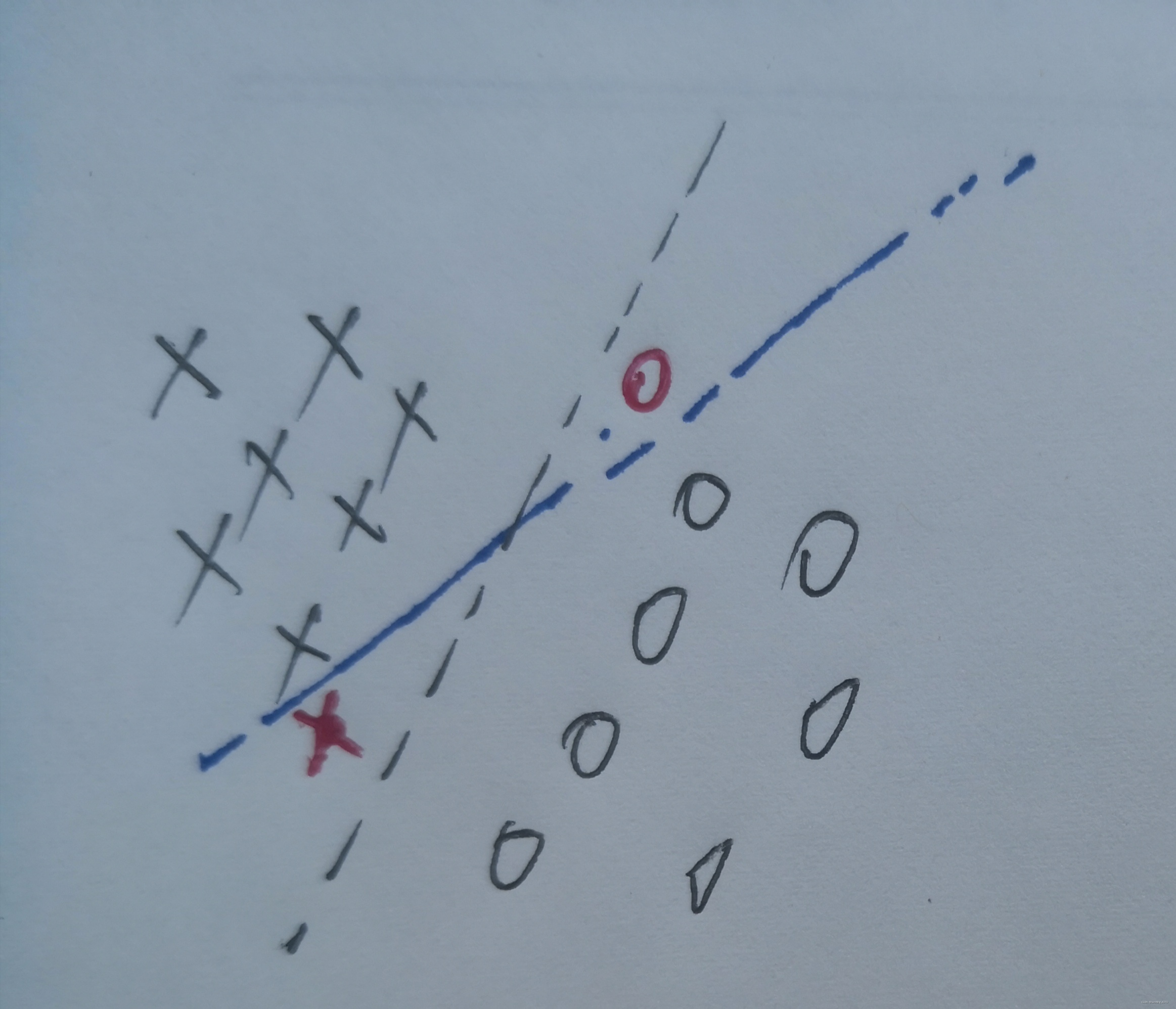
• 间隔增大意味着对于样本的容错能力增强，因此SVM方法的核心目标即为最大化间隔

  如下图，黑色间隔平面与样本间间隔较大，蓝色平面与样本间隔较小，对于红色新样本点，黑色平面分类结果更合理：

形式描述(二分类)

• 有输入样本集$X=[x_1,x_2,...,x_n]$，对应标签 L = [ y 1 , y 2 , . . . , y n ] , y i ∈ { + 1 , − 1 } L=[y_1,y_2,...,y_n],y_i\in{\{+1,-1\}} L=[y1​,y2​,...,yn​],yi​∈{+1,−1}

• 在d维空间中有分割平面$(w,b)$，其与输入样本的间隔为$\tau$

• 优化目标为：
  $$\underset{W,b}{argmax}\tau$$

• 确定分割超平面$(w,b)$后，定义分类器为：
  $$\overline{y_i}=sign(w{x}_i+b)$$

相关概念

• 间隔：

  • 函数间隔

    • 定义函数间隔：
      $$\begin{gathered} \overline{{\tau }_i}=y_i(w{x}_i+b) \\ \bar{\tau }=min(\overline{{\tau }_i}) \end{gathered}$$

    • 可以通过函数间隔的正负判断分类正误，由于$(\lambda w,\lambda b)$代表同一个平面，该值大小无确切物理意义

  • 几何间隔

    • 定义物理间隔：
      $$\begin{gathered} {\tau }_i=y_i(\frac{w{x}_i}{|w|}+\frac{b}{|w|}) \\ \tau =min({\tau }_i) \end{gathered}$$

    • 几何间隔值即为空间中样本点$x_i$到分割平面的距离

  • 软间隔&硬间隔

    • 硬间隔：

      • 最大化间隔问题可以表示为：
        $$\begin{gathered} \underset{w,b}{argmax}\tau \\ s.t.y_i(\frac{w{x}_i}{|w|}+\frac{b}{|w|})\ge \tau \end{gathered}$$
        该问题的约束，即要求训练集样本线性可分，目标超平面可以完美划分训练集中两类样本的

        这种情况，即为存在硬间隔

    • 软间隔：

      • 若训练集中样本非严格线性可分，无法找到一个超平面完美地将两类样本分开，使用硬间隔的方法无法处理

      • 调整对于决策边界的定义，让决策边界能够忍受一小部分训练误差，在最大化间隔与减少被分错的样本数之间寻求平衡

      • 在约束中引入松弛变量，即
        $$y_i(\frac{w{x}_i}{|w|}+\frac{b}{|w|})\ge \tau -{\xi }_i$$

    • 这种方案下，引入松弛变量的间隔问题称为软间隔

    • 两类样本间不存在直线能将其完美分开，即$y_i(\frac{w{x}_i}{|w|}+\frac{b}{|w|})\ge \tau$约束无法满足，为解决这种情况，只能引入松弛变量${\xi }_i$，使带松弛的约束成立

  • KKT条件

    • 定理:

      对有等式及不等式约束的问题：
      $$\begin{array}{rl}& minf(x)\\ s.t.& g_j(x)\le 0(j=1,2,...,m)\\ & h_k(x)=0(k=1,2,...,l)\end{array}$$
      KKT条件给出判断$x^{\ast }$是否为最优解的必要条件（当原问题为凸问题时也是必要条件）
      $$\{\begin{array}{l}\frac{\partial f}{\partial x_i}+{\sum }_{j=1}^d{u}_j\frac{\partial g_j}{\partial x_i}+{\sum }_{k=1}^l{\lambda }_k\frac{\partial h_k}{\partial x_i}=0(i=1,2,...,n)\\ h_k(x)=0\\ g_j(x)\le 0\\ u_j{g}_j(x)=0\\ u_j\ge 0,{\lambda }_j\ne 0\end{array}$$

    • 推导：见数学推导部分

    • 理解：

      • 相等约束在空间中构成一个曲面，不等约束构成曲面加曲面一侧空间

        

      • 对一个满足单约束的点$x^{\ast }$，其可行方向（在这些方向上移动一点，点仍然近似满足约束）

        • 满足$h(x)=0$，可行方向为约束曲面在$x^{\ast }$处的切面$T_h$
        • 满足$g(x)\le 0$，且$g(x^{\ast })<0$，可行方向为全空间
        • 满足$g(x)\le 0$，且$g(x^{\ast })=0$，可行方向为切面$T_g$（保持为0）与$g(x)$的负梯度方向（约束内部空间）

      • 多约束情况：
        

        • 满足多个约束的点的可行方向是每个约束的可行方向的交集

      • 对最小化$f(x)$问题，满足各约束的$f(x)$的取值空间在函数平面与各约束的交集上，即可行空间由多个约束切面的法向量张成

      • 对满足所有约束的$x^{\ast }$点
        $$f(x^{\ast })的可行方向由\frac{\partial g_i}{\partial x}{|}_{x^{\ast }}(i=1,2,...,m)张成$$

      • $f(x)$在$x^{\ast }$处约束下的梯度为函数梯度与约束切面的法向量的线性组合：
        $$\frac{\partial f}{\partial x}+\sum _{j=1}^d{u}_j\frac{\partial g_j}{\partial x}$$

      • 由于规定不等约束小于0，而不等式约束梯度指向不等式函数增加方向（球外,大于0），为保证约束条件，规定：
        $$u_j\le 0$$

  • 对偶问题

    • 原始问题
      $$\begin{array}{rl}& minf(x)\\ s.t.& g_j(x)\le 0(j=1,2,...,m)\\ & h_k(x)=0(k=1,2,...,l)\end{array}$$

      • 拉格朗日函数

      $$L(x,\alpha ,\beta )=f(x)+\sum _{i=1}^m{\alpha }_i{g}_i(x)+\sum _{i=1}^l{\beta }_i{h}_i(x)$$

      ​ 定义：
      $${\theta }_p(x)=\underset{\alpha ,\beta }{\max }L(x,\alpha ,\beta )$$
      ​ 有：
      $${\theta }_p(x)=\{\begin{array}{l}f(x)(x满足约束)\\ +\infty else\end{array}$$
      ​ 因此，极小化问题
      $$min{\theta }_p(x)=\underset{x}{\min }\underset{\alpha ,\beta }{\max }L(x,\alpha ,\beta )$$
      ​ 称作广义拉格朗日函数的极小极大问题，与约束下极小化问题等价

      • 定义原始问题最优解$P^{\ast }=\underset{x}{\min }{\theta }_p(x)$

    • 对偶问题：

      • 定义
        $${\theta }_D(\alpha ,\beta )=\underset{x}{\min }L(x,\alpha ,\beta )$$
        极大化：
        $$\underset{\alpha ,\beta }{\max }{\theta }_D(\alpha ,\beta )=\underset{\alpha ,\beta }{\max }\underset{x}{\min }L(x,\alpha ,\beta )$$
        称作广义拉格朗日函数的极大极小问题，也称作原始问题的对偶问题

      • 对偶问题的最优解$d^{\ast }=\underset{\alpha ,\beta }{\max }{\theta }_D(\alpha ,\beta )$

      • 原始问题与对偶问题关系：

        • 若原始问题与对偶问题均有最优值，有：

        $$d^{\ast }=\underset{\alpha ,\beta }{\max }\underset{x}{\min }L(x,\alpha ,\beta )\le \underset{x}{\min }\underset{\alpha ,\beta }{\max }L(x,\alpha ,\beta )=p^{\ast }$$

        • 设${\alpha }^{\ast },{\beta }^{\ast },x^{\ast }$为原始问题和对偶问题可行解，且$d^{\ast }=p^{\ast }$，则${\alpha }^{\ast },{\beta }^{\ast },x^{\ast }$是原始问题与对偶问题最优解
        • 假设$f(x)$与$g_i(x)$是凸函数，$h_i(x)$是仿射函数，有$g_i(x)<0$ ，则存在${\alpha }^{\ast },{\beta }^{\ast },x^{\ast }$，使$x^{\ast }$是原始问题解，${\alpha }^{\ast },{\beta }^{\ast }$是对偶问题解

方法推导

• 硬间隔

  • 根据硬间隔方法定义，优化目标为：

  $$\begin{gathered} \underset{w,b}{argmax}\tau \\ s.t.y_i(\frac{w{x}_i}{|w|}+\frac{b}{|w|})\ge \tau \end{gathered}$$

  • 由函数间隔定义，目标可改为：
    $$\begin{gathered} \underset{W,b}{argmax}\frac{\bar{\tau }}{|w|} \\ s.t.y_i(w{x}_i+b)\ge \bar{\tau } \end{gathered}$$

  • 由于函数间隔不由点和平面唯一确定，指定距离平面最近的样本点到平面函数距离为1，即$\bar{\tau }=1$ ，有：
    $$\begin{gathered} \underset{W,b}{argmax}\frac{1}{|w|} \\ s.t.y_i(w{x}_i+b)-1\ge 0 \end{gathered}$$

  • 该问题又可转化为：
    $$\begin{gathered} \underset{w,b}{argmin}\frac{1}{2}|w{|}^2 \\ s.t.y_i(w{x}_i+b)-1\ge 0 \end{gathered}$$

  • 构建广义拉格朗日函数：
    $$L(x,\alpha ,\beta )=\frac{1}{2}|w{|}^2-\sum _{i=1}^n{\alpha }_i{y}_i(w{x}_i+b)+\sum _{i=1}^n{\alpha }_i$$
    原问题等价于：
    $$\underset{W,b}{\min }\underset{\alpha }{\max }L(w,b,\alpha )$$
    原问题的对偶问题：
    $$\underset{\alpha }{\max }\underset{W,b}{\min }L(w,b,\alpha )$$

  • $\underset{W,b}{\min }L(W,b,\alpha )$求解：

    • 求偏导，令为0
      $$L(x,\alpha ,\beta )=\frac{1}{2}|w{|}^2-\sum _{i=1}^n{\alpha }_i{y}_i(w{x}_i+b)+\sum _{i=1}^n{\alpha }_i$$

      $$\{\begin{array}{l}{\nabla }_{w}L(w,b,\alpha )=w-{\sum }_{i=1}^n{\alpha }_i{y}_i{x}_i=0\\ {\nabla }_{b}L(w,b,\alpha )=-{\sum }_{i=1}^n{\alpha }_i{y}_i=0\end{array}$$

    • 得：
      $$\{\begin{array}{l}w={\sum }_{i=1}^n{\alpha }_i{y}_i{x}_i\\ {\sum }_{i=1}^n{\alpha }_i{y}_i=0\end{array}$$
      带入L，有：
      $$\begin{array}{rl}L(x,\alpha ,\beta )& =\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i{x}_j)-\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{y}_i((\sum _{i=1}^n{\alpha }_i{y}_i{x}_i)x_i+b)+\sum _{i=1}^n{\alpha }_i\\ & =-\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i{x}_j)+\sum _{i=1}^n{\alpha }_i\end{array}$$

  • 求$\underset{W,b}{\max }{\theta }_D$：
    $$\underset{\alpha }{\max }\underset{w,b}{\min }L(W,b,\alpha )$$

    $$\begin{array}{rl}\underset{\alpha }{\max }(-\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n& {\alpha }_i{\alpha }_j{y}_i{y}_j(x_i{x}_j)+\sum _{i=1}^n{\alpha }_i)\\ s.t.& \sum _{i=1}^n{\alpha }_i{y}_i=0\\ & {\alpha }_i\ge 0\end{array}$$

    转化为
    $$\begin{array}{rl}\underset{\alpha }{\min }(\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n& {\alpha }_i{\alpha }_j{y}_i{y}_j(x_i{x}_j)-\sum _{i=1}^n{\alpha }_i)\\ s.t.& \sum _{i=1}^n{\alpha }_i{y}_i=0\\ & {\alpha }_i\ge 0\end{array}$$
    上述问题也是原始问题的对偶问题

  • 结合对偶问题相关定理，目标函数与约束函数为凸函数，约束严格可行，故存在${\alpha }^{\ast },w^{\ast },b^{\ast }$使 ${\alpha }^{\ast }$是原问题的解，$w^{\ast },b^{\ast }$是对偶问题的解

  • 因此，有线性可分数据集，已知对偶问题解${\alpha }^{\ast }=({\alpha }_1^{\ast },{\alpha }_2^{\ast },...,{\alpha }_n^{\ast })$，即可求得原始问题解$w^{\ast },b^{\ast }$：

    由KKT条件：
    $$\{\begin{array}{l}{\nabla }_{w}L(w,b,\alpha )=w-{\sum }_{i=1}^n{\alpha }_i{y}_i{x}_i=0\\ {\nabla }_{b}L(w,b,\alpha )=-{\sum }_{i=1}^n{\alpha }_i{y}_i=0\\ {\alpha }_i^{\ast }(y_i(w^{\ast }{x}_i+b^{\ast })-1)=0\\ y_i(w^{\ast }{x}_i+b^{\ast })-1\ge 0\\ {\alpha }_i^{\ast }\ge 0\end{array}$$
    得：
    $$\{\begin{array}{l}{w}^{\ast }={\sum }_{i=1}^n{\alpha }_i^{\ast }{y}_i{x}_i\\ b_j^{\ast }=y_j-{\sum }_{i=1}^n{\alpha }_i^{\ast }{y}_i{x}_i{x}_j(j满足{\alpha }_j>0)\end{array}$$

  • 对偶问题求解${\alpha }^{\ast }$通过SMO方法完成

• 软间隔

  为了处理线性不可分情况，修改约束条件，对样本点$x_i$引入松弛变量${\zeta }_i$，有：
  $$y_i(w{x}_i+b)\ge 1-{\zeta }_i$$
  优化目标为：
  $$\begin{gathered} \underset{w,b,\zeta }{\min }\frac{1}{2}|w{|}^2+C\sum _{i=1}^n{\zeta }_i \\ s.t.y_i(w{x}_i+b)\ge 1-{\zeta }_i(i=1,2,...n) \\ {\zeta }_i\ge 0 \end{gathered}$$
  广义拉格朗日函数：
  $$L(w,b,\zeta ,\alpha ,u)=\frac{1}{2}|w{|}^2+C\sum _{i=1}^n{\zeta }_i-\sum _{i=1}^n{\alpha }_i(y_i(w{x}_i+b)-1+{\zeta }_i)-\sum _{i=1}^n{u}_i{\zeta }_i$$
  目标问题是极小极大问题：
  $$\underset{W,b,\zeta }{\min }\underset{\alpha ,u}{\max }L(w,b,\zeta ,\alpha ,u)$$
  对偶问题为极大极小问题：
  $$\underset{\alpha ,u}{\max }\underset{w,b,\zeta }{\min }L(w,b,\zeta ,\alpha ,u)$$

  • 先求极小$\underset{w,b,\zeta }{\min }L(w,b,\zeta ,\alpha ,u)$：

    • 令偏导为0
      $$\{\begin{array}{l}{\nabla }_{w}L(w,b,\zeta ,\alpha ,u)=w-{\sum }_{i=1}^n{\alpha }_i{y}_i{x}_i=0\\ {\nabla }_{b}L(w,b,\zeta ,\alpha ,u)=-{\sum }_{i=1}^n{\alpha }_i{y}_i=0\\ {\nabla }_{{\zeta }_i}L(w,b,\zeta ,\alpha ,u)=C-{\alpha }_i-u_i=0\end{array}$$

    • 得：
      $$\{\begin{array}{l}w={\sum }_{i=1}^n{\alpha }_i{y}_i{x}_i\\ {\sum }_{i=1}^n{\alpha }_i{y}_i=0\\ C-{\alpha }_i-u_i=0\end{array}$$

    • 带回L得：
      $$L(w,b,\zeta ,\alpha ,u)=-\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i{x}_j+\sum _{i=1}^n{\alpha }_i$$
      有约束：
      $$\begin{gathered} \sum _{i=1}^n{\alpha }_i{y}_i=0 \\ 0\le {\alpha }_i\le C \end{gathered}$$

  • 再对极小求极大，问题为：
    $$\begin{gathered} \underset{\alpha }{\max }(-\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i{x}_j+\sum _{i=1}^n{\alpha }_i) \\ s.t.\sum _{i=1}^n{\alpha }_i{y}_i=0 \\ 0\le {\alpha }_i\le C \end{gathered}$$
    该问题是原问题的对偶问题

  • 目标函数与约束函数为凸函数，约束严格可行，故存在${\alpha }^{\ast },w^{\ast },b^{\ast }$使 ${\alpha }^{\ast }$是原问题的解，$w^{\ast },b^{\ast }$是对偶问题的解

    由KKT条件：
    $$\{\begin{array}{l}{\nabla }_{w}L(w,b,\zeta ,\alpha ,u)=w-{\sum }_{i=1}^n{\alpha }_i{y}_i{x}_i=0\\ {\nabla }_{b}L(w,b,\zeta ,\alpha ,u)=-{\sum }_{i=1}^n{\alpha }_i{y}_i=0\\ {\nabla }_{{\zeta }_i}L(w,b,\zeta ,\alpha ,u)=C-{\alpha }_i-u_i=0\\ {\alpha }_i^{\ast }(y_i(w^{\ast }{x}_i+b^{\ast })-1+{\zeta }_i)=0\\ u_i{\zeta }_i=0\\ y_i(w{x}_i+b)-1+{\zeta }_i\ge 0\\ {\zeta }_i\ge 0,{\alpha }_i\ge 0,u_i\ge 0\end{array}$$
    在对偶问题解${\alpha }^{\ast }$确定情况下，有：
    $$\begin{array}{rl}& w^{\ast }=\sum _{i=1}^n{\alpha }_i{y}_i{x}_i\\ & b_j^{\ast }=y_j-\sum _{i=1}^n{y}_i{\alpha }_i^{\ast }(x_i{x}_j)(0<{\alpha }_j<C,u_j\ne 0,{\zeta }_j=0)\end{array}$$

  • 对偶问题求解${\alpha }^{\ast }$通过SMO方法完成

• SMO方法

  • 求解目标：

    • ${\alpha }^{\ast }=({\alpha }_1^{\ast },...,a_n^{\ast })$

    $$\begin{gathered} \underset{\alpha }{\min }(\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_{j}K(x_i{x}_j)-\sum _{i=1}^n{\alpha }_i) \\ s.t.\sum _{i=1}^n{\alpha }_i{y}_i=0 \\ 0\le {\alpha }_i\le C \end{gathered}$$

  • 基本思路：

    • 若${\alpha }^{\ast }$中所有变量解都满足KKT条件，则${\alpha }^{\ast }$满足KKT条件
    • SMO算法将原问题不断分为子问题并对其求解
    • 每个子问题更新时指定两个变量，一个是违反KKT条件最严重的变量${\alpha }_1$，另一个由${\alpha }_2=-y_1{\sum }_{i\ne 2}{\alpha }_i{y}_i$确定

  • 变量更新：

    • 选取一对变量${\alpha }_1,{\alpha }_2$

    • 优化目标：
      $$\begin{gathered} \underset{{\alpha }_1,{\alpha }_2}{\min }W({\alpha }_1,{\alpha }_2)=\frac{1}{2}{K}_{11}{\alpha }_1^2+\frac{1}{2}{K}_{22}{\alpha }_2^2+y_1{y}_2{K}_{12}{\alpha }_1{\alpha }_2-({\alpha }_1+{\alpha }_2)+y_1{\alpha }_1\sum _{i=3}^n{y}_i{\alpha }_i{K}_{i1}+y_2{\alpha }_2\sum _{i=3}^n{y}_i{\alpha }_i{K}_{i2} \\ s.t.{\alpha }_1{y}_1+{\alpha }_2{y}_2=-\sum _{i=3}^n{y}_i{\alpha }_i=\zeta \\ 0\le {\alpha }_i\le C \end{gathered}$$

    • ${\alpha }_1,{\alpha }_2$之间的约束关系可表示为：

      

      两个变量存在限制，因此两变量优化问题实际上是单变量优化问题，假设对${\alpha }_2$进行优化，上一轮解为${\alpha }_1^{old},{\alpha }_2^{old}$，假设沿着约束方向未根据约束剪切的解是${\alpha }_2^{new,unc}$，本轮结果${\alpha }_1^{new},{\alpha }_2^{new}$

      假设L,H分别为${\alpha }_2^{new}$所在线段的边界，有$L<{\alpha }_2^{new}<H$

      若是左图中的情况($y_1,y_2$不一致)，
      $$L=max(0,{\alpha }_2^{old}-{\alpha }_1^{old}),H=min(C,C+{\alpha }_2^{old}-{\alpha }_1^{old})$$
      若是右图中的情况($y_1,y_2$一致)，
      $$L=max(0,{\alpha }_2^{old}+{\alpha }_1^{old}-C),H=min(C,{\alpha }_2^{old}+{\alpha }_1^{old})$$
      有：
      $${\alpha }_2^{new}=\{\begin{array}{l}H{\alpha }_2^{new,unc}>H\\ {\alpha }_2^{new,unc}L<{\alpha }_2^{new,unc}<H\\ L{\alpha }_2^{new,unc}<L\end{array}$$

    • ${\alpha }_2^{new,unc}$求解

      • 定义：

      $$\begin{array}{rl}& g(x)=\sum _{j=1}^m{\alpha }_j^{\ast }{y}_{j}K(x_j,x_i)+b\\ & E_i(x)=g(x_i)-y_i\\ & v_i=\sum _{i=3}^n{y}_j{\alpha }_{j}K(x_i,x_j)=g(x_i)-\sum _{i=1}^2{\alpha }_j^{\ast }{y}_{j}K(x_j,x_i)-b\end{array}$$

      • 目标函数简化为：
        $$W({\alpha }_1,{\alpha }_2)=\frac{1}{2}{K}_{11}{\alpha }_1^2+\frac{1}{2}{K}_{22}{\alpha }_2^2+y_1{y}_2{K}_{12}{\alpha }_1{\alpha }_2-({\alpha }_1+{\alpha }_2)+y_1{\alpha }_1{v}_1+y_2{\alpha }_2{v}_2$$

      • 由：
        $$\begin{gathered} {\alpha }_1{y}_1+{\alpha }_2{y}_2=\zeta \\ {y}_i^2=1 \end{gathered}$$
        有：
        $${\alpha }_1=y_1(\zeta -{\alpha }_2{y}_2)$$

      • 再带入目标，消除${\alpha }_1$：
        $$W({\alpha }_2)=\frac{1}{2}{K}_{11}(y_1(\zeta -{\alpha }_2{y}_2){)}^2+\frac{1}{2}{K}_{22}{\alpha }_2^2+y_2{K}_{12}{\alpha }_2(\zeta -{\alpha }_2{y}_2)-y_1(\zeta -{\alpha }_2{y}_2)-{\alpha }_2+(\zeta -{\alpha }_2{y}_2)v_1+y_2{\alpha }_2{v}_2$$
        对${\alpha }_2$求导，令为0：
        $$\frac{\partial W}{\partial {\alpha }_2}=K_{11}{\alpha }_2+K_{22}{\alpha }_2-2K_{12}{\alpha }_2-K_{11}\zeta y_2+K_{12}\zeta y_2+y_1{y}_2-1-v_1{y}_2+v_2{y}_2=0$$
        再带入${\alpha }_1{y}_1+{\alpha }_2{y}_2=\zeta$，求解得：
        $${\alpha }_2^{new,unc}={\alpha }_2^{old}+\frac{y2(E_1-E_2)}{K_{11}+K_{22}-2K_{12}}$$

    • 阈值与差值更新：

      • 完成两个变量的优化之后，需要重新计算阈值b

      • 当$0<{\alpha }_1^{new}<C$有：$y_1-{\sum }_{i=1}^n{\alpha }_i{y}_i{K}_{i1}-b_1=0$

      • 新的$b_1^{new}$与$E_1$
        $$b_1^{new}=y_1-\sum _{i=3}^n{\alpha }_i{y}_i{K}_{i1}-{\alpha }_1^{new}{y}_1{K}_{11}-{\alpha }_2^{new}{y}_2{K}_{21}$$

        $$E_1=g(x_1)-y_1={\alpha }_1^{old}{y}_1{K}_{11}+{\alpha }_2^{old}{y}_2{K}_{21}+\sum _{i=3}^n{\alpha }_i{y}_i{K}_{i1}+b^{old}-y_1$$

        $$b_1^{new}=-E_1-y_1{K}_{11}({\alpha }_1^{new}-{\alpha }_2^{old})-y_2{K}_{21}({\alpha }_2^{new}-{\alpha }_2^{old})+b^{old}$$

      • 同样，$0<{\alpha }_2^{new}<C$时有$b_2^{new}$
        $$b_2^{new}=-E_2-y_1{K}_{12}({\alpha }_1^{new}-{\alpha }_1^{old})-y_2{K}_{22}({\alpha }_2^{new}-{\alpha }_2^{old})+b^{old}$$

      • $$b^{new}=\frac{b_1^{new}+b_2^{new}}{2}$$

      • 更新$E_i$
        $$E_i=\sum _{支持向量}{y}_j{\alpha }_{j}K(x_i,x_j)+b^{new}-y_i$$

  • 变量选择：

    • 第一个变量:

      检测样本$(x_i,y_i)$是否满足KKT条件：
      $$\{\begin{array}{l}\begin{array}{rl}{\alpha }_i=0& <=>y_i(\sum _{j=1}^n{\alpha }_j{y}_{j}K(x_j{x}_i)+b)\ge 1(间隔外)\\ 0<{\alpha }_i<C& <=>y_i(\sum _{j=1}^n{\alpha }_j{y}_{j}K(x_j{x}_i)+b)=1(间隔边界上的支持向量)\\ {\alpha }_i=C& <=>y_i(\sum _{j=1}^n{\alpha }_j{y}_{j}K(x_j{x}_i)+b)\le 1(间隔内)\end{array}\end{array}$$
      优先选间隔超平面上的点（支持向量），若这些点都满足KKT条件，再选其他违反KKT条件的点

    • 第二个变量：

      假设我们在外层循环已经找到了${\alpha }_1$, 第二个变量${\alpha }_2$的选择标准是让$|E_1-E_2|$尽可能大，即当$E_1$正时选最小的$E_i$，否则选最大$E_i$

  • SMO流程：

    • 取初值${\alpha }^0=0,k=0$
    • 选取${\alpha }_1^k,{\alpha }_2^k$
    • 计算${\alpha }_2^{k+1},{\alpha }_1^{k+1}$
    • 计算$b^{k+1}$与$E_i$
    • 若对所有${\alpha }_i$均满足KKT条件，结束，否则回到第二步

• 多分类：

  • SVM方法是基于几何的方法，只能通过多个分割平面组合来解决多分类问题，有OVO,OVA两种方案

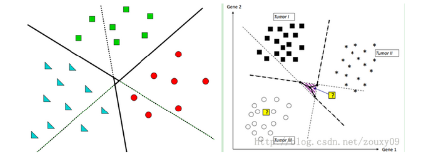
  • OVO（One Vs One）

    • 对于每两类之间，都求一个分割超平面（求K(K-1)/2个平面*）

      

    • 在判断样本分类情况时，对所有的分割平面都进行一次判断，投票决定分类（进行K(K-1)/2次判断*）

  • OVA（One Vs All）

    • 对每一类样本，都视作本类与非本类的二分类问题，求一个分割平面（整个样本集求K个平面）

    

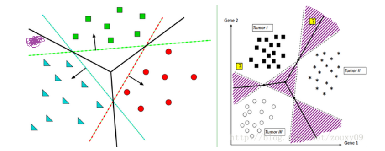
    • 判断样本分类时，对所有的分割平面都进行一次判断，投票决定分类（进行K次判断）

  • 二者相比，OVO方法无法判断的区域比OVA方法小，更加准确，但计算量更大

方法流程

• 输入数据集$X=[x_1,x_2,...,x_n]$，标签$L=[y_1,y_2,...,y_n]$

• 选择惩罚系数C，构造约束优化问题：
  $$\begin{gathered} \underset{\alpha }{\min }(\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i{x}_j+\sum _{i=1}^n{\alpha }_i) \\ s.t.\sum _{i=1}^n{\alpha }_i{y}_i=0 \\ 0\le {\alpha }_i\le C \end{gathered}$$

• SMO算法求出目标最小时${\alpha }^{\ast }$

• 计算$w^{\ast }={\sum }_{i=1}^n{\alpha }_i{y}_i{x}_i$

• 找出支撑向量对应$(x_j,y_j)$，计算对应$b_j^{\ast }=y_j-{\sum }_{i=1}^n{y}_i{\alpha }_i^{\ast }(x_i{x}_j)(0<{\alpha }_j<C,u_j\ne 0,{\zeta }_j=0)$

  $b^{\ast }=\frac{1}{S}{\sum }_j{b}_j^{\ast }$

• 分割超平面为：
  $$w^{\ast }x+b^{\ast }=0$$
  分类器：
  $$f(x)=sign(w^{\ast }x+b^{\ast })$$

参考资料

【1】《统计学习方法》 李航

【2】支持向量机原理(四)SMO算法原理