参考链接：https://leetcode-cn.com/problems/paths-with-sum-lcci/solution/yi-pian-wen-zhang-jie-jue-suo-you-er-cha-w3hu/

问题分类

二叉树路径的问题大致可以分为两类：
1、自顶向下：
顾名思义，就是从某一个节点(不一定是根节点)，从上向下寻找路径，到某一个节点(不一定是叶节点)结束
具体题目如下：
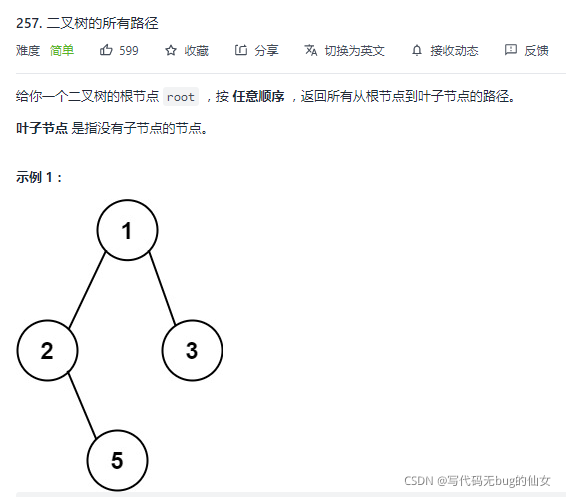
257. 二叉树的所有路径
面试题 04.12. 求和路径
112. 路径总和
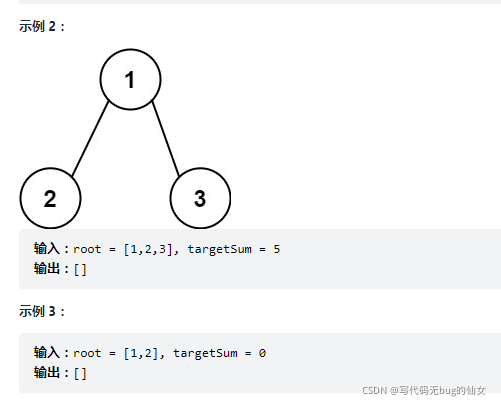
113. 路径总和 II
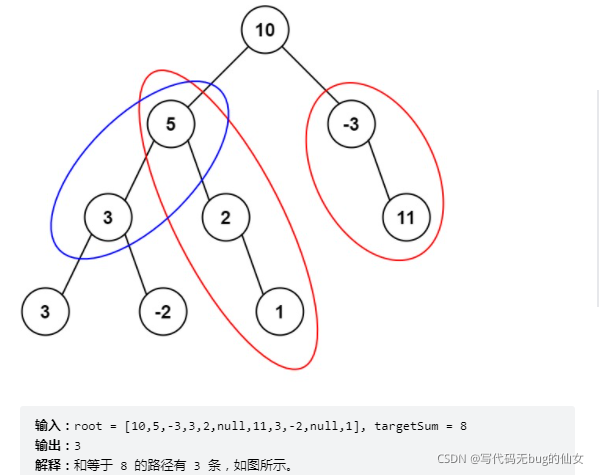
437. 路径总和 III
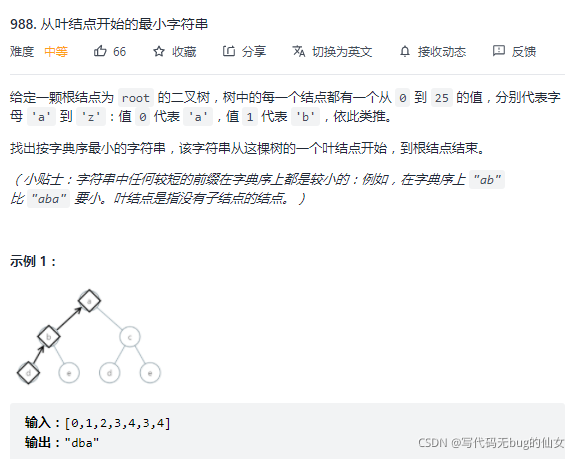
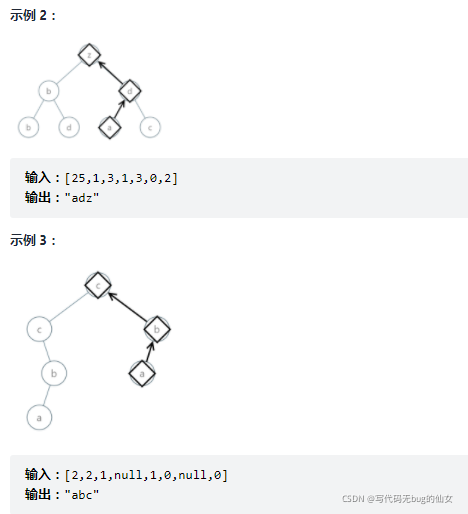
988. 从叶结点开始的最小字符串

而继续细分的话还可以分成一般路径与给定和的路径

2、非自顶向下：
就是从任意节点到任意节点的路径，不需要自顶向下
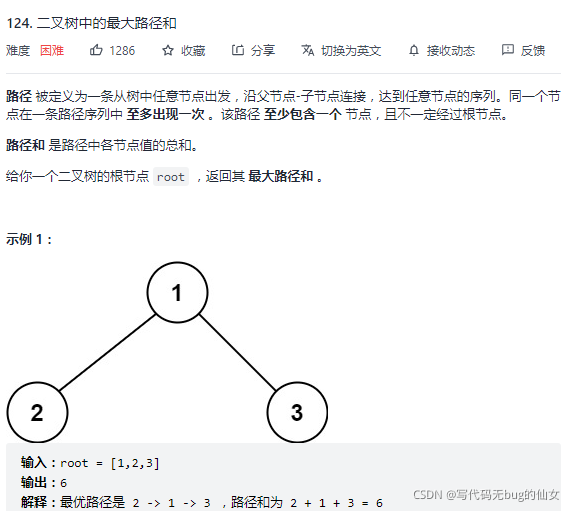
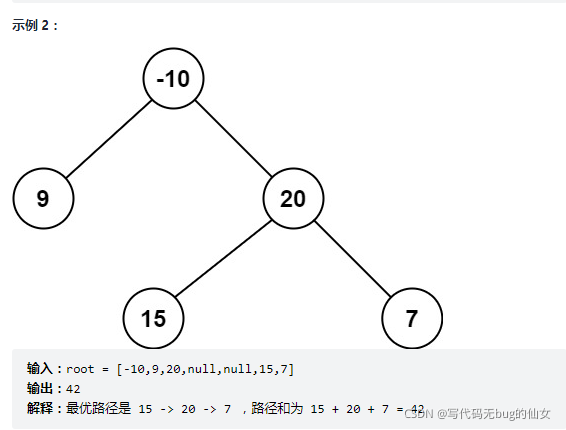
124. 二叉树中的最大路径和
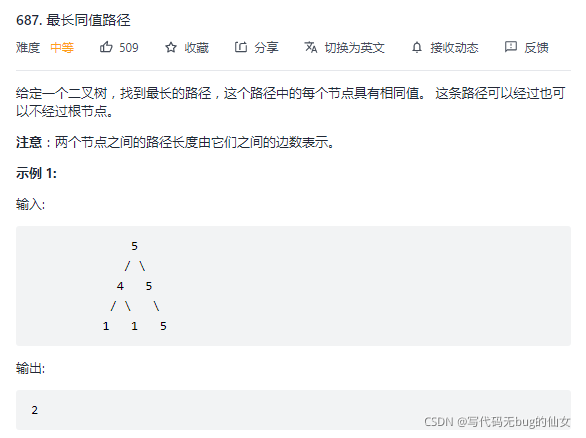
687. 最长同值路径
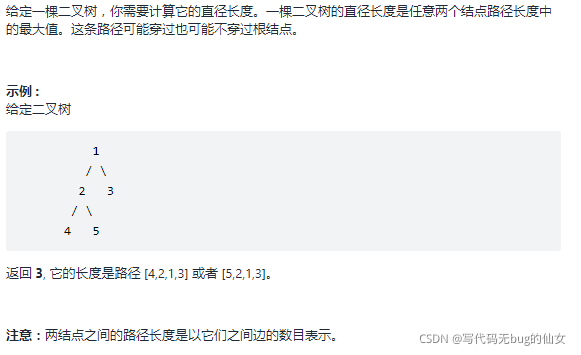
543. 二叉树的直径

解题模板

这类题通常用深度优先搜索(DFS)和广度优先搜索(BFS)解决，BFS较DFS繁琐，这里为了简洁只展现DFS代码
一、自顶而下：
dfs

一般路径：
vector<vector<int>>res;
void dfs(TreeNode*root,vector<int>path)
{
    if(!root) return;  //根节点为空直接返回
    path.push_back(root->val);  //作出选择
    if(!root->left && !root->right) //如果到叶节点  
    {
        res.push_back(path);
        return;
    }
    dfs(root->left,path);  //继续递归
    dfs(root->right,path);
}

# **给定和的路径：**
void dfs(TreeNode*root, int sum, vector<int> path)
{
    if (!root)
        return;
    sum -= root->val;
    path.push_back(root->val);
    if (!root->left && !root->right && sum == 0)
    {
        res.push_back(path);
        return;
    }
    dfs(root->left, sum, path);
    dfs(root->right, sum, path);
}

二、非自顶而下：

这类题目一般解题思路如下：
设计一个辅助函数maxpath，调用自身求出以一个节点为根节点的左侧最长路径left和右侧最长路径right，那么经过该节点的最长路径就是left+right
接着只需要从根节点开始dfs,不断比较更新全局变量即可

int res=0;
int maxPath(TreeNode *root) //以root为路径起始点的最长路径
{
    if (!root)
        return 0;
    int left=maxPath(root->left);
    int right=maxPath(root->right);
    res = max(res, left + right + root->val); //更新全局变量  
    return max(left, right);   //返回左右路径较长者
}

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<string>res;
    vector<string> binaryTreePaths(TreeNode* root) {
        dfs(root,"");
        return res;
    }
    void dfs(TreeNode*root,string path){
        if(!root){
            return ;
        }
        path += to_string(root->val);//把根节点加入路径
        if(!root->left && !root->right){//到达叶节点
            res.push_back(path);//路径加入结果中
            return;
        }
        dfs(root->left,path+"->");//继续遍历
        dfs(root->right,path+"->");
    }
};

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>>res;
    vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
        vector<int>path;
        dfs(root,targetSum,path);
        return res;
    }
    void dfs(TreeNode* root,int sum,vector<int>path){
        if(!root){
            return;
        }
        sum -= root->val;
        path.push_back(root->val);
        if(!root->left && !root->right && sum == 0){
            res.push_back(path);
            return;
        } 
        dfs(root->left,sum,path);
        dfs(root->right,sum,path);

    }
};

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int count;
    int pathSum(TreeNode* root, int targetSum) {
        if(!root){
            return 0;
        }
        dfs(root,targetSum); //以root为起始点查找路径
        pathSum(root->left,targetSum);//左子树递归
        pathSum(root->right,targetSum);//右子树递归
        return count;
    }
    void dfs(TreeNode* root,int sum){
        if(!root){
            return;
        }
        sum -= root->val;
        if(sum == 0){//注意不要return,因为不要求到叶节点结束,所以一条路径下面还可能有另一条
            count++;//如果找到了一个路径全局变量就+1
        }
        dfs(root->left,sum);
        dfs(root->right,sum);
    }
};

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<string>res;
    string smallestFromLeaf(TreeNode* root) {
        dfs(root,"");
        sort(res.begin(),res.end());//升序排列
        return res[0];//返回第一个路径
    }
    void dfs(TreeNode* root,string path){
        if(!root){
            return ;
        }
        path += 'a'+root->val;//0：a,加上a就等于转换字母
        if(!root->left && !root->right){
            reverse(path.begin(),path.end());//从叶节点到根节点
            res.push_back(path);
            return;
        } 
        dfs(root->left,path);
        dfs(root->right,path);
    }
};

二、非自顶向下

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int res = INT_MIN; //注意节点值可能为负数，因此要设置为最小值
    int maxPathSum(TreeNode* root) {
        maxPath(root);
        return res;

    }
    // left,right分别为根节点左右子树最大路径和,注意：如果最大路径和<0,意味着该路径和对总路径和做负贡献，因此不要计入到总路径中，将它设置为0
    int maxPath(TreeNode* root){ //以root为路径起始点的最长路径
        if(!root){
            return 0;
        }
        int left = max(maxPath(root->left),0);
        int right = max(maxPath(root->right),0);
        res = max(res,left+right+root->val);//比较当前最大路径和与左右子树最长路径加上根节点值的较大值，更新全局变量
        return max(root->val+left,root->val+right);
    }
};

687. 最长同值路径
     

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int res;
    int longestUnivaluePath(TreeNode* root) {
        longestPath(root);
        return res;

    }
    int longestPath(TreeNode* root){
        if(!root){
            return 0;
        }
        int left = longestPath(root->left);
        int right = longestPath(root->right);
        // 如果存在左子节点和根节点同值，更新左最长路径;否则左最长路径为0
        if(root->left && root->val == root->left->val){
            left++;
        }else{
            left = 0;
        }
        if(root->right && root->val == root->right->val){
            right++;
        }else{
            right = 0;
        }
        res = max(res,left+right);
        return max(left,right);

    }
};

543. 二叉树的直径
     

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int res;
    int diameterOfBinaryTree(TreeNode* root) {
        maxPath(root);
        return res;
    }
    int maxPath(TreeNode* root){
        if(!root){
            return 0;
        }
        int left = maxPath(root->left);
        int right = maxPath(root->right);
        if(root->left){
            left++;
        }
        if(root->right){
            right++;
        }
        res = max(left+right,res);
        return max(left,right);
    }
};