该章总结

BRDF模型，这是一种基于物理的分析模型，创建的光照模型效果较好
BRDF的理解
基于物理着色：BRDF

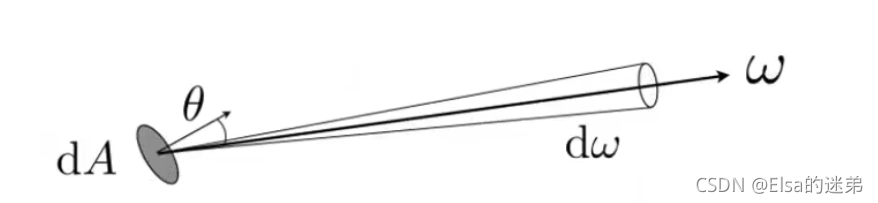
微分立体角

含义：在某个三维方向上，θ和Φ各移动一个微小位移。

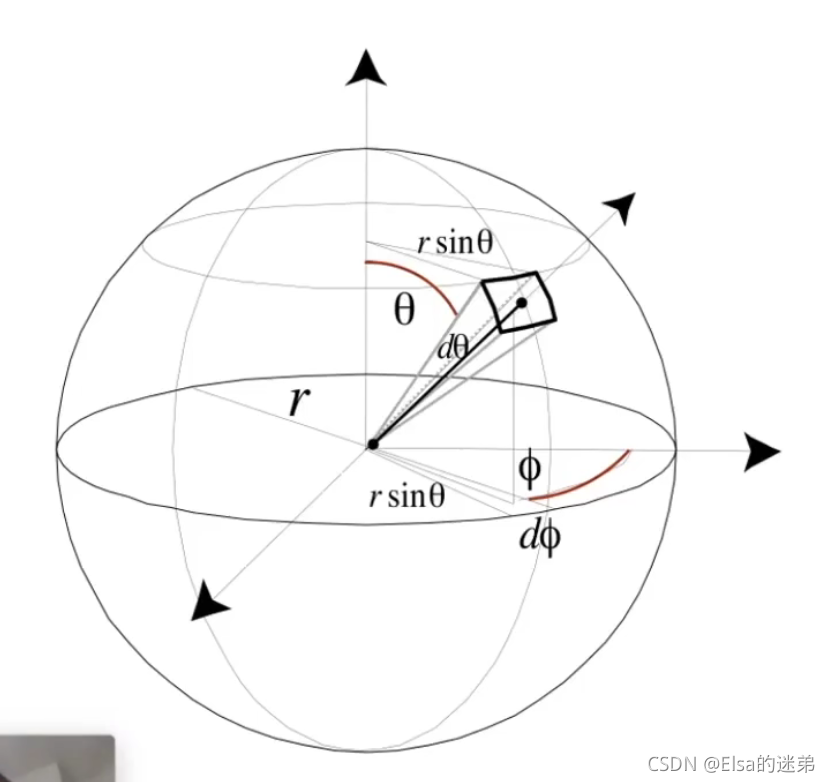
则这个微小位移所包含的表面积可近似为

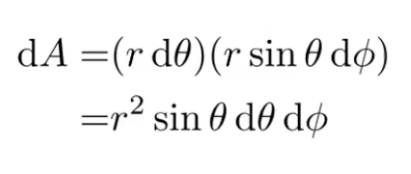
微分立体角即为微分角所包含的表面积除以r的平方
即：

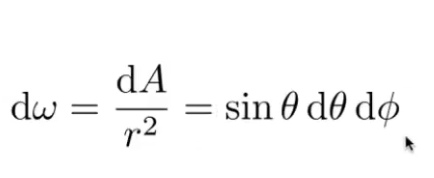
irradiance(power per unit area)

辐射度: 单位面积（垂直于光线）上的辐射通量

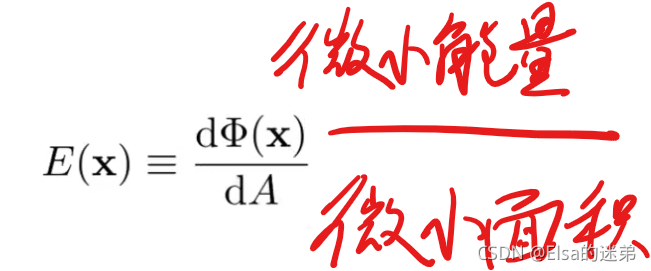
单位

瓦特/平方米

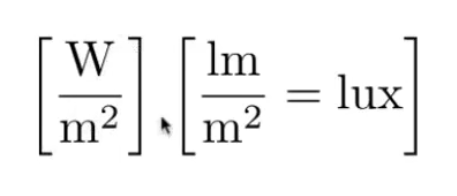
注意

若某个面与光线不垂直，则需要将该面变为与光线垂直投影面。（与我们处理漫反射相似）

irradiance Falloff(辐射度衰减)

变的不是立体角，而是立体角对应的面积。
当该面积距离辐照中心为r时，面积为单位圆上对应面积的r平方倍。
故：
若在单位圆上有辐射度E为

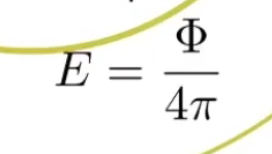
则在半径为r的圆上，辐射度为

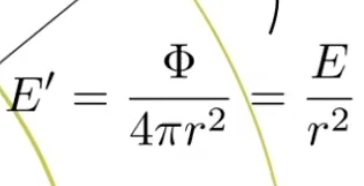
Radiance

定义：在单位面积上向单位立体角辐射的能量

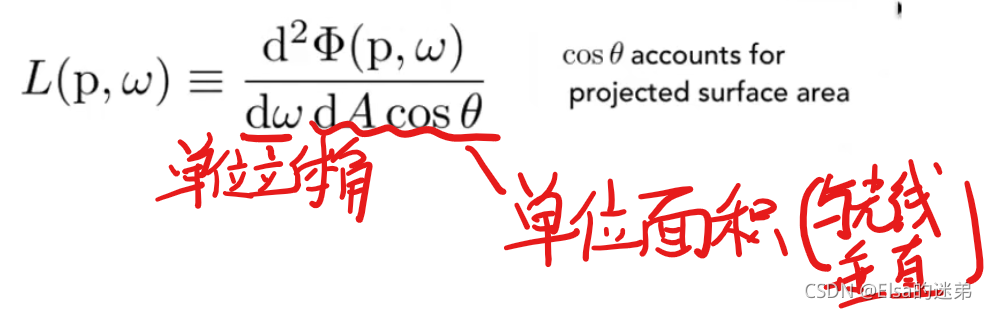
理解：某个单位区域向某一个确定的方向辐射的能量

Irradiance & Radiance

Irradiance 某一个小面积（dA）收到的能量是多少。
Radiance 只考虑某一个方向（dw）进来让小面积（dA）受到的能量

可以看出，Radiance 是在 Irradiance 上确定了一个入射光线的方向

BRDF （双向反射分布函数）

Bidirectional Reflectance Distribution Function
用来解决： 已知入射光的能量和角度，求出给定方向的辐射的能量是多少

渲染方程

从反射方程推出的更加通用的方程

• wi 为入射方向
• w0 为反射方向
• p为反射点
• n为法线 (wi,n)为两法线间的余弦值
• L为光线强度
• f为BRDF函数

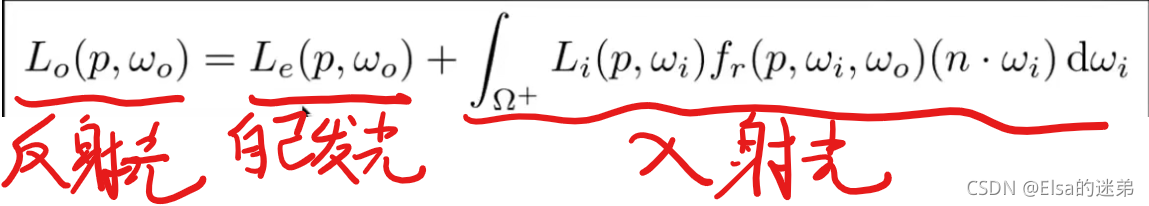这么解这个方程？？？？？ 下节课讲解！！！

若入射光为多个线光源，可直接相加求和
若入射光为面光源，可以积分求解
若入射光来自一个面的反射，则将反射面作为一个面光源求解

这便是光线弹射多次的原理

下节课的基础知识

随机变量
期望值
概率密度函数

使用概率论方法解渲染方程