文章目录
- 二叉树OJ淬体
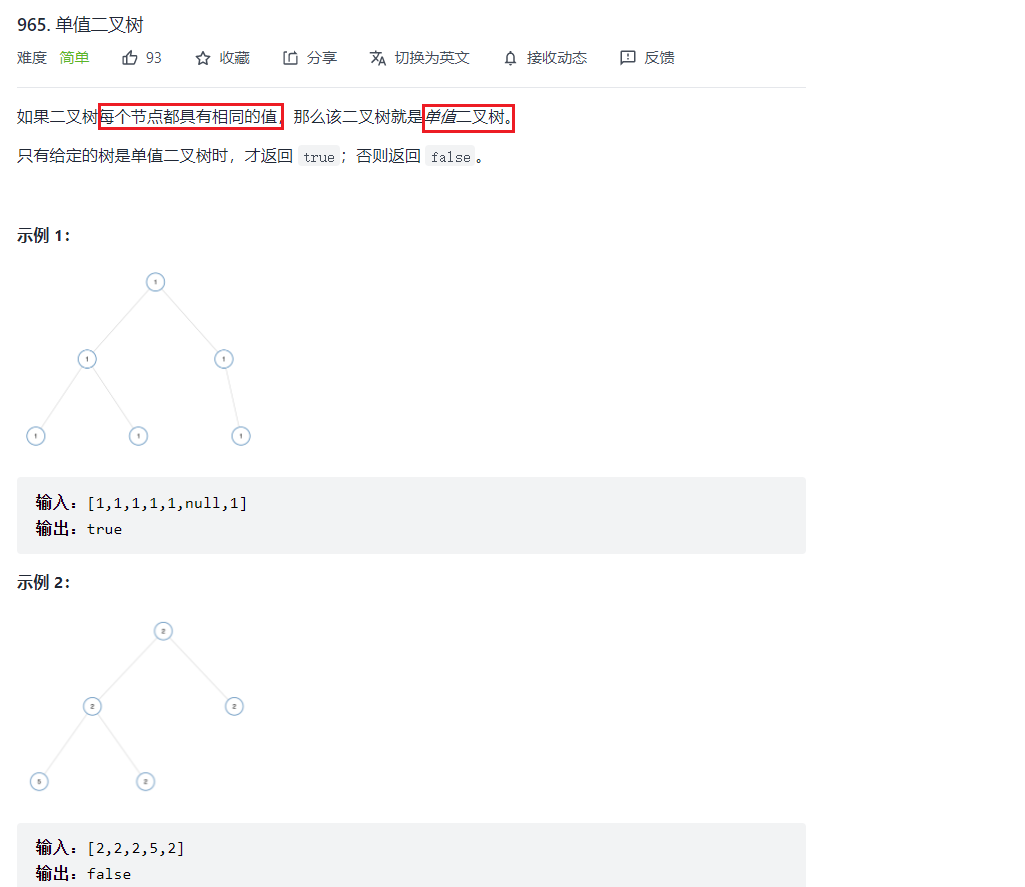
- 例1:[单值二叉树](https://leetcode-cn.com/problems/univalued-binary-tree/)
-
- 例2:[二叉树的前序遍历](https://leetcode-cn.com/problems/binary-tree-preorder-traversal/)
-
- 例3:[二叉树的中序遍历](https://leetcode-cn.com/problems/binary-tree-inorder-traversal/)
-
- 例4:[二叉树的后序遍历](https://leetcode-cn.com/problems/binary-tree-postorder-traversal/)
-
- 例5:[相同的树](https://leetcode-cn.com/problems/same-tree/)
-
- 例6:[对称二叉树](https://leetcode-cn.com/problems/symmetric-tree/)
-
- 例7:[另一棵树的子树](https://leetcode-cn.com/problems/subtree-of-another-tree/)
-
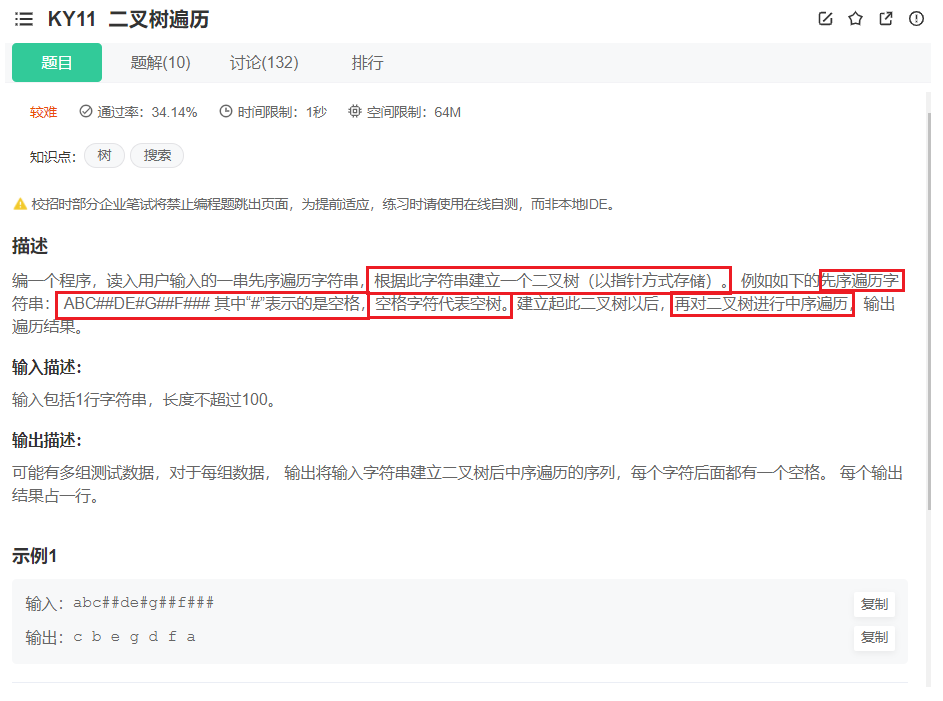
- 例8:[二叉树遍历](https://www.nowcoder.com/practice/4b91205483694f449f94c179883c1fef?tpId=60&&tqId=29483&rp=1&ru=/activity/oj&qru=/ta/tsing-kaoyan/question-ranking)
-

二叉树OJ淬体
题目
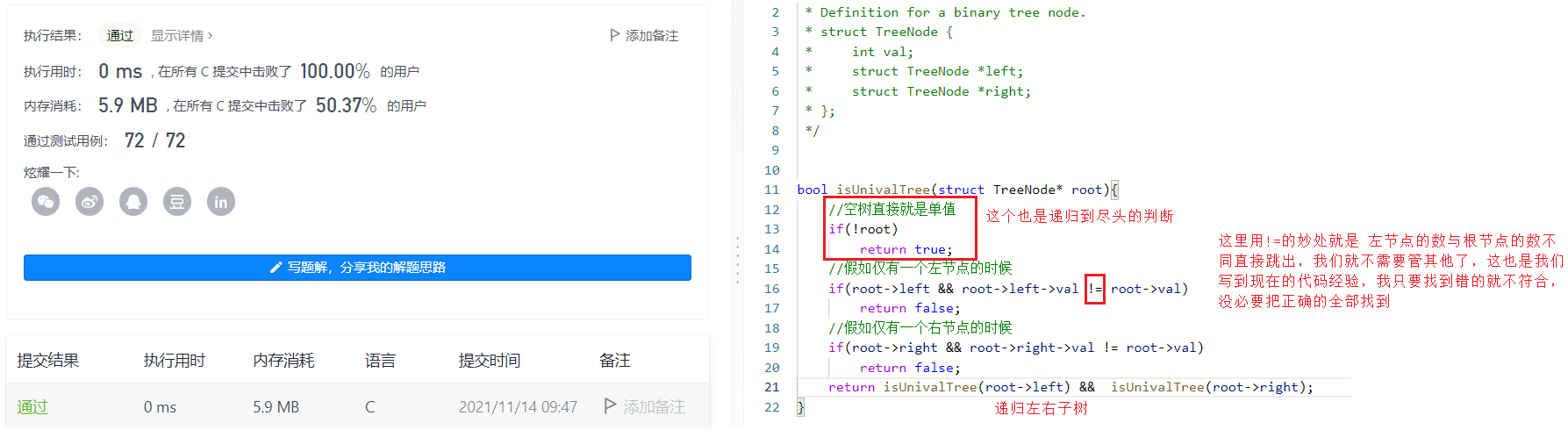
bool isUnivalTree(struct TreeNode* root){
if(!root)
return true;
if(root->left && root->left->val != root->val)
return false;
if(root->right && root->right->val != root->val)
return false;
return isUnivalTree(root->left) && isUnivalTree(root->right);
}
题目
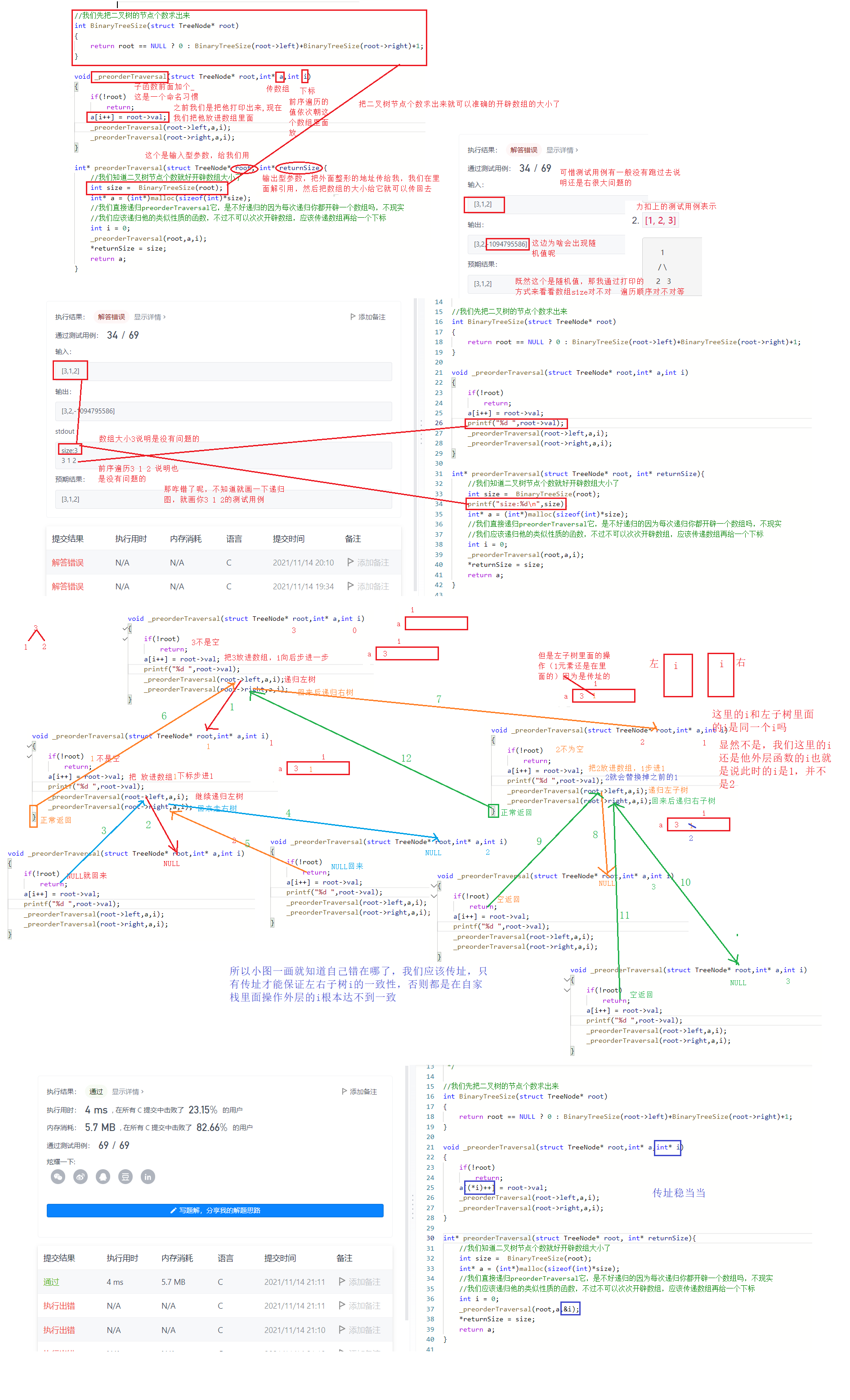
int BinaryTreeSize(struct TreeNode* root)
{
return root == NULL ? 0 : BinaryTreeSize(root->left)+BinaryTreeSize(root->right)+1;
}
void _preorderTraversal(struct TreeNode* root,int* a,int* i)
{
if(!root)
return;
a[(*i)++] = root->val;
_preorderTraversal(root->left,a,i);
_preorderTraversal(root->right,a,i);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize){
int size = BinaryTreeSize(root);
int* a = (int*)malloc(sizeof(int)*size);
int i = 0;
_preorderTraversal(root,a,&i);
*returnSize = size;
return a;
}
题目
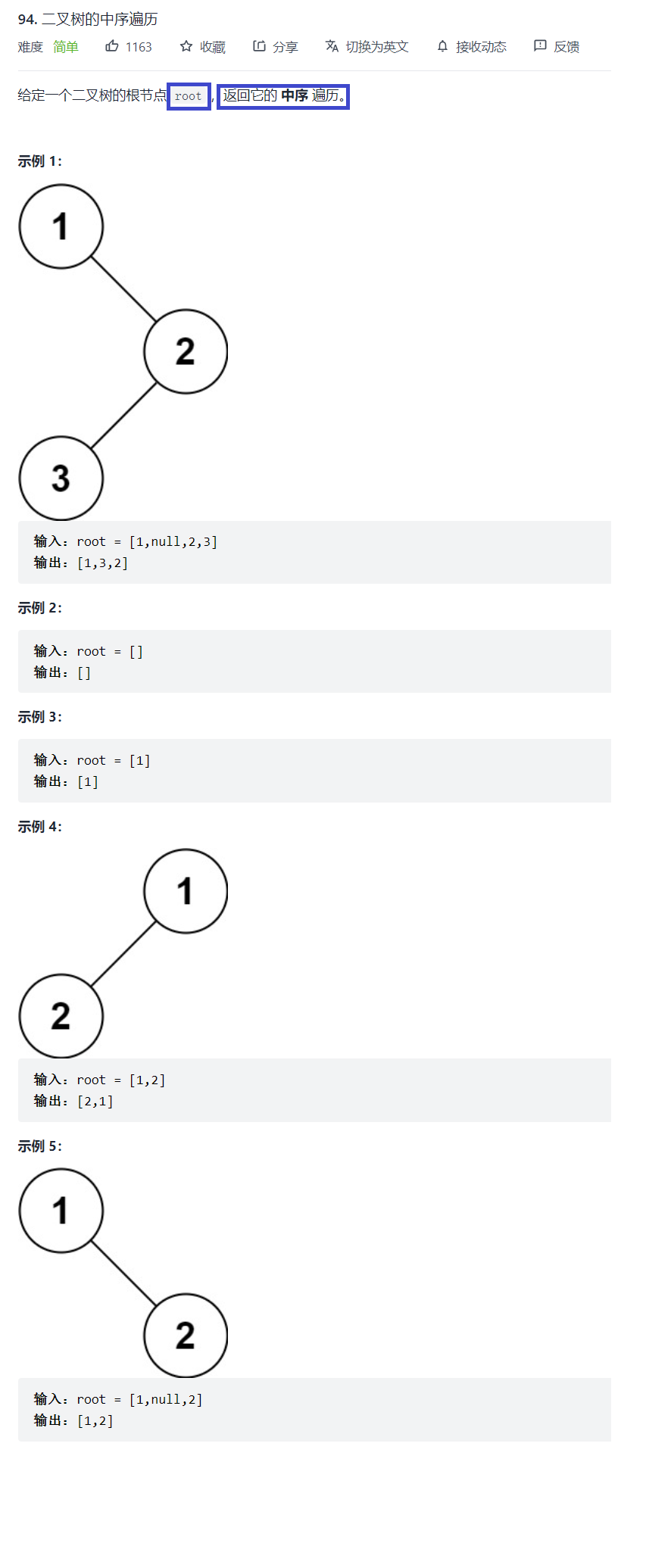
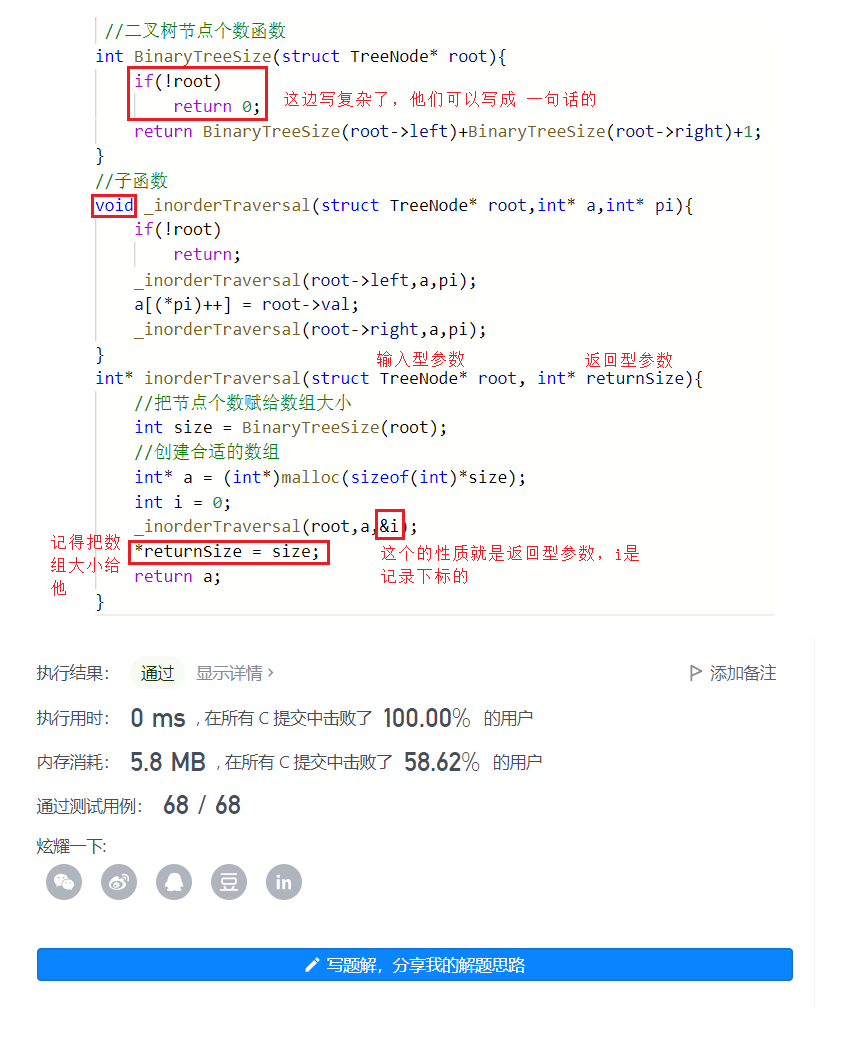
int BinaryTreeSize(struct TreeNode* root){
if(!root)
return 0;
return BinaryTreeSize(root->left)+BinaryTreeSize(root->right)+1;
}
void _inorderTraversal(struct TreeNode* root,int* a,int* pi){
if(!root)
return;
_inorderTraversal(root->left,a,pi);
a[(*pi)++] = root->val;
_inorderTraversal(root->right,a,pi);
}
int* inorderTraversal(struct TreeNode* root, int* returnSize){
int size = BinaryTreeSize(root);
int* a = (int*)malloc(sizeof(int)*size);
int i = 0;
_inorderTraversal(root,a,&i);
*returnSize = size;
return a;
}
题目
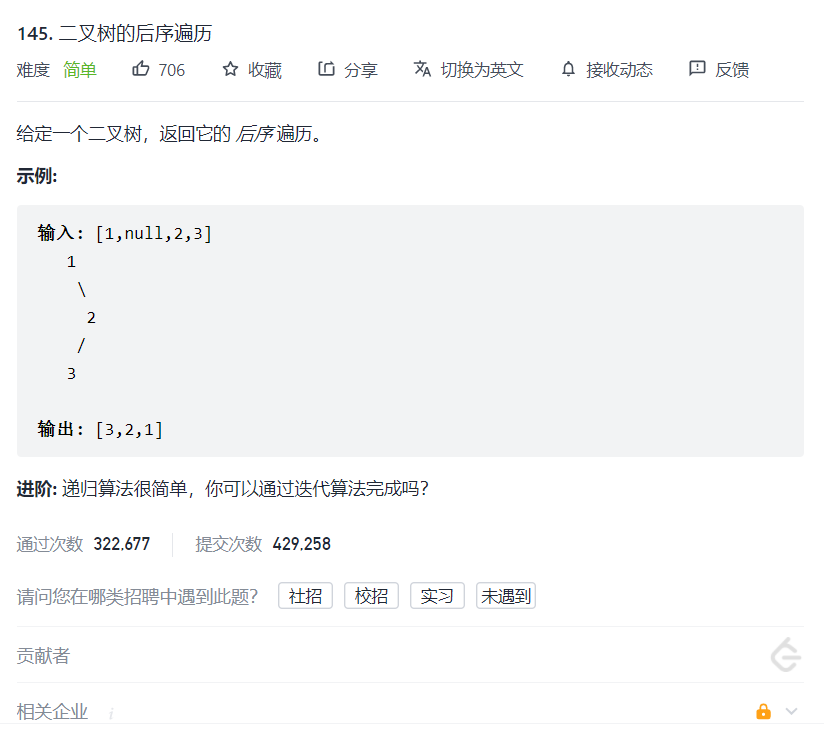
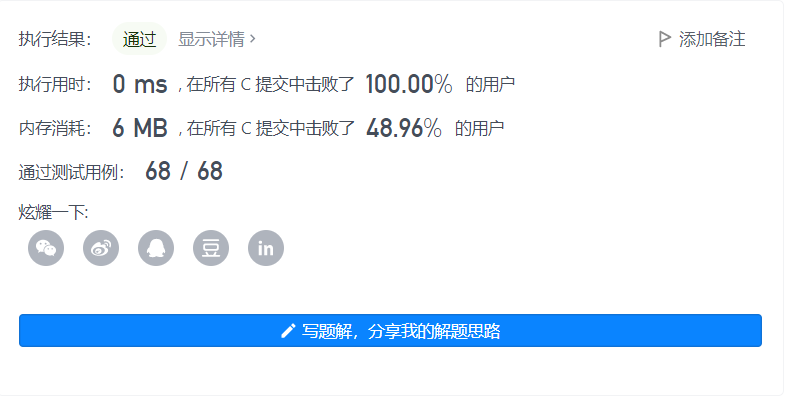
int BinaryTreeSize(struct TreeNode* root){
return root == NULL ? 0 : BinaryTreeSize(root->left)+BinaryTreeSize(root->right)+1;
}
void _postorderTraversal(struct TreeNode* root,int* a,int* pi){
if(!root)
return;
_postorderTraversal(root->left,a,pi);
_postorderTraversal(root->right,a,pi);
a[(*pi)++] = root->val;
}
int* postorderTraversal(struct TreeNode* root, int* returnSize){
int size = BinaryTreeSize(root);
int* a = (int*)malloc(sizeof(int)*size);
int i = 0;
_postorderTraversal(root,a,&i);
*returnSize = size;
return a;
}
题目
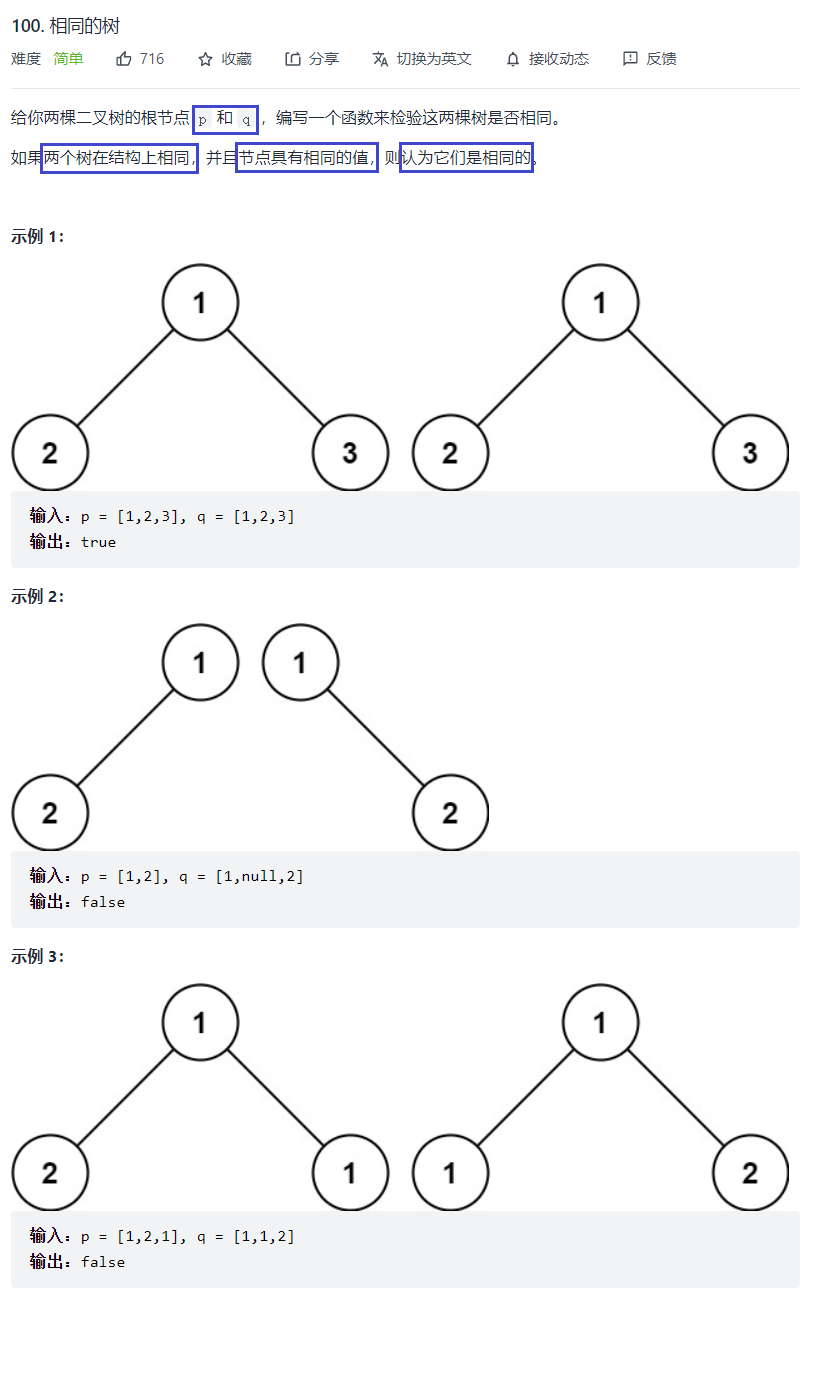
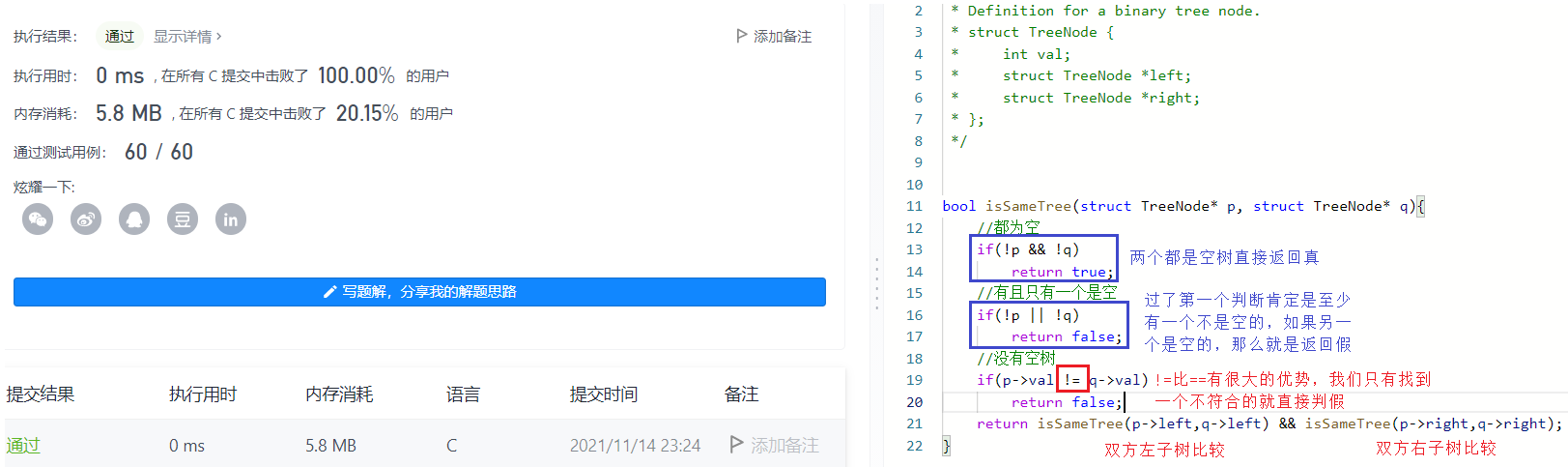
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
if(!p && !q)
return true;
if(!p || !q)
return false;
if(p->val != q->val)
return false;
return isSameTree(p->left,q->left) && isSameTree(p->right,q->right);
}
题目
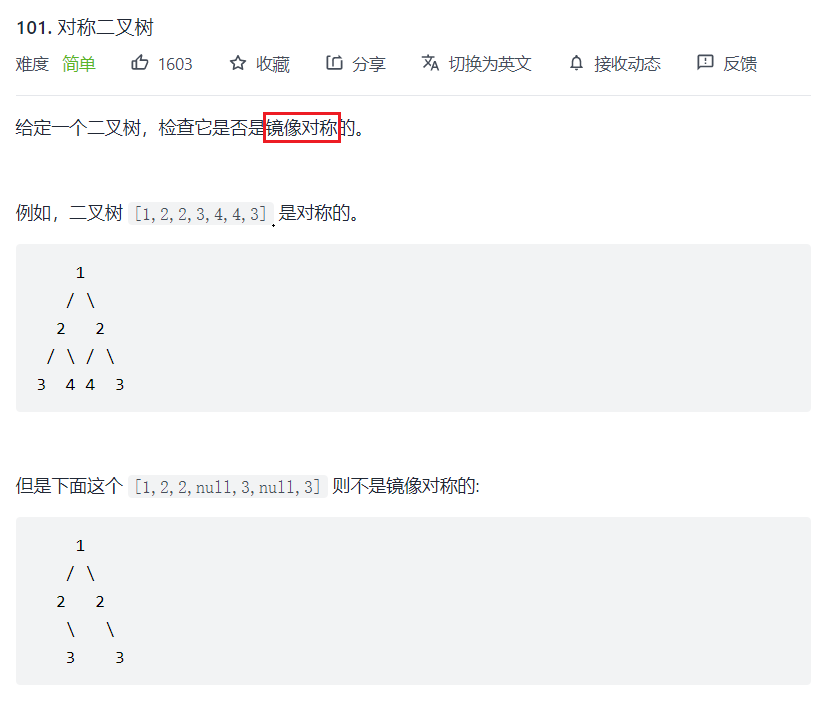
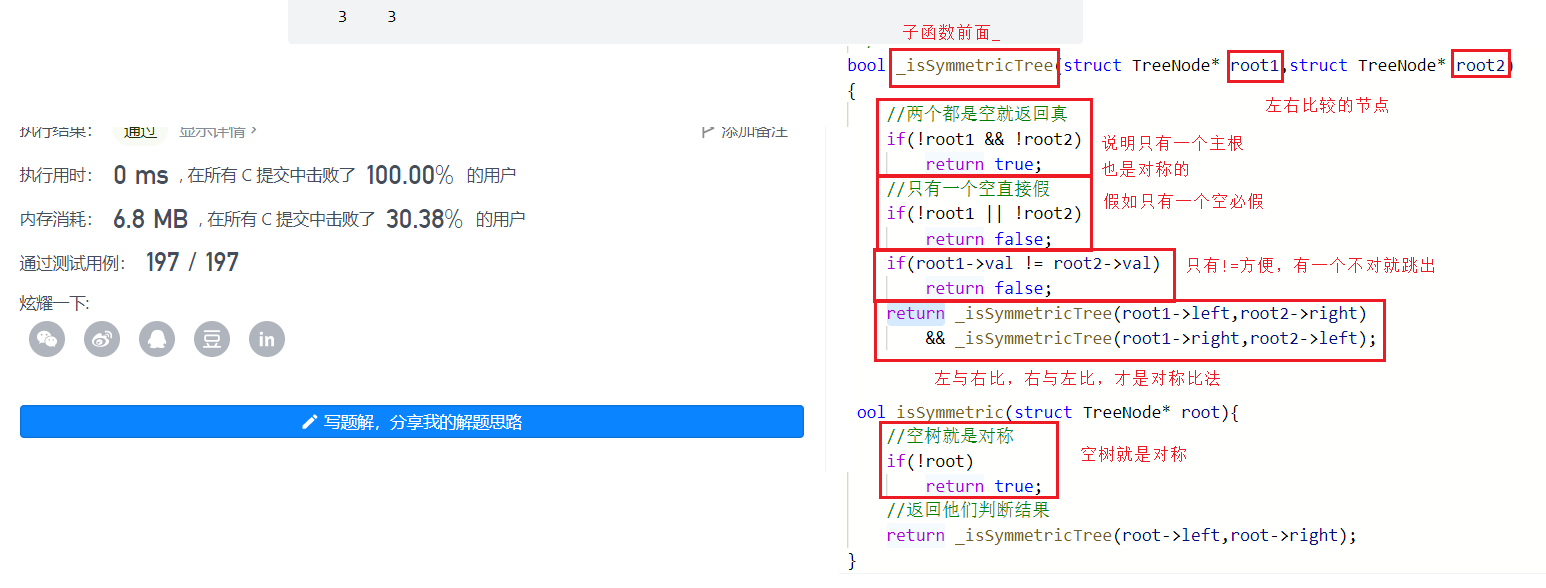
bool _isSymmetricTree(struct TreeNode* root1,struct TreeNode* root2)
{
if(!root1 && !root2)
return true;
if(!root1 || !root2)
return false;
if(root1->val != root2->val)
return false;
return _isSymmetricTree(root1->left,root2->right)
&& _isSymmetricTree(root1->right,root2->left);
}
bool isSymmetric(struct TreeNode* root){
if(!root)
return true;
return _isSymmetricTree(root->left,root->right);
}
题目
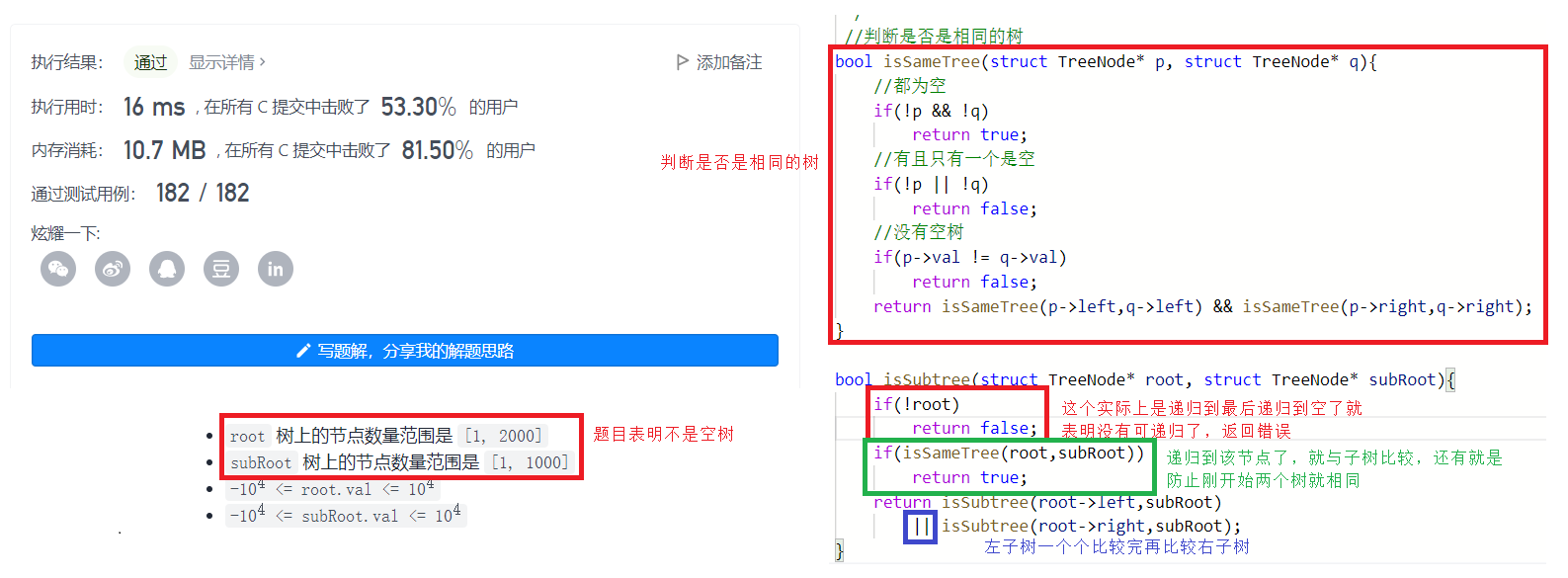
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
if(!p && !q)
return true;
if(!p || !q)
return false;
if(p->val != q->val)
return false;
return isSameTree(p->left,q->left) && isSameTree(p->right,q->right);
}
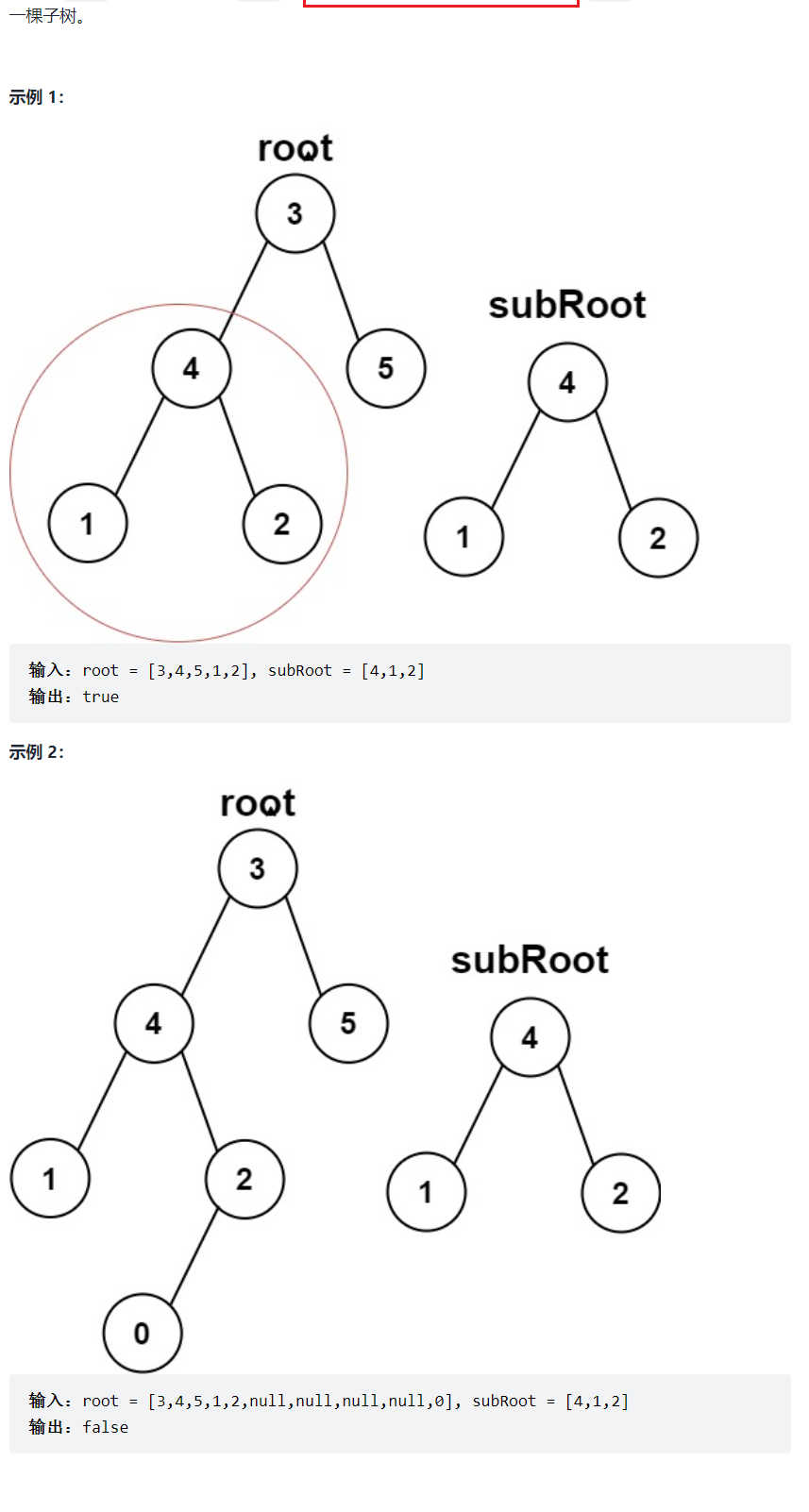
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
if(!root)
return false;
if(isSameTree(root,subRoot))
return true;
return isSubtree(root->left,subRoot)
|| isSubtree(root->right,subRoot);
}
题目