4076. 字符串权值【签到】

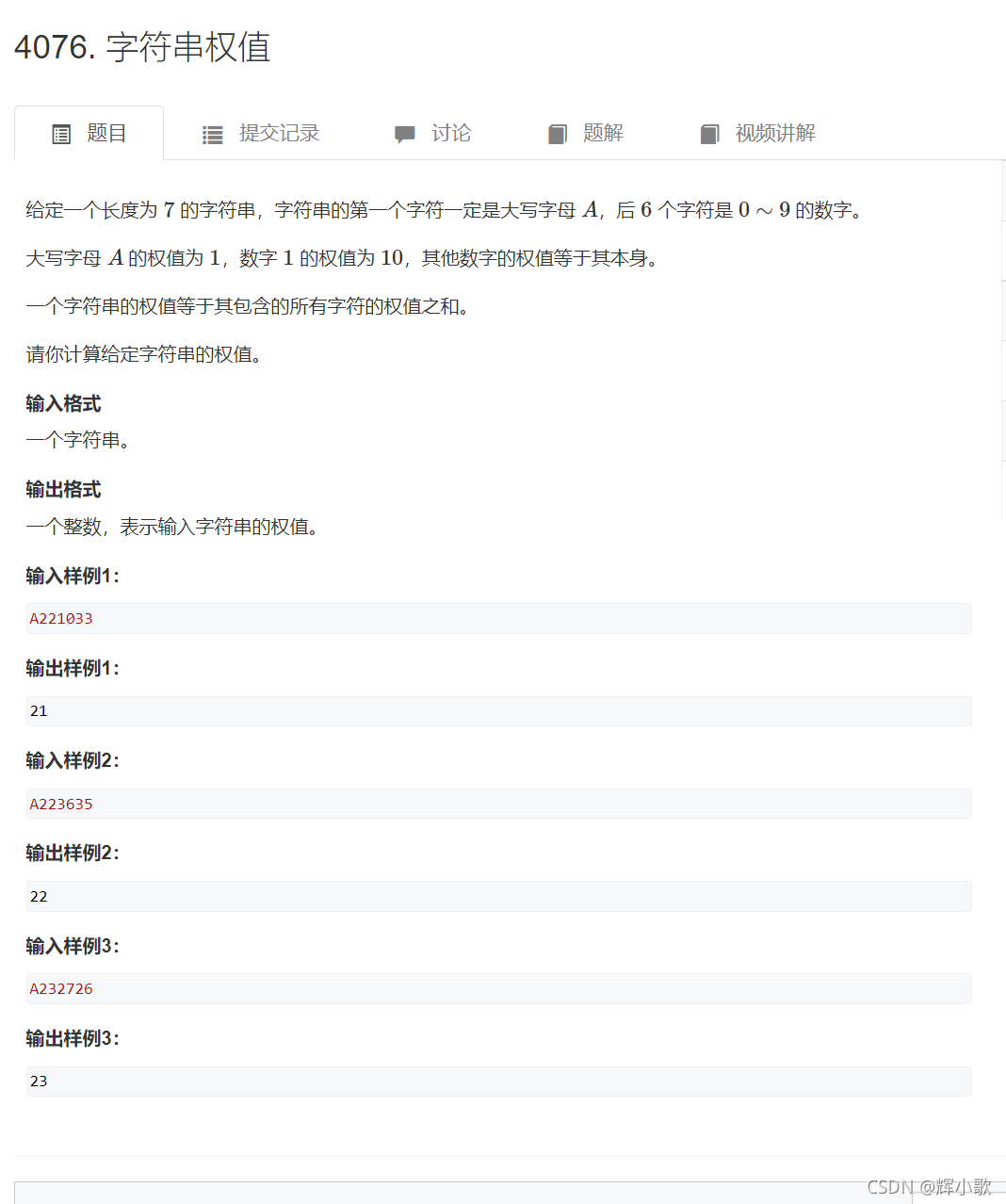
https://www.acwing.com/problem/content/4079/

#include<bits/stdc++.h>
using namespace std;
int main(void)
{
    string s; cin>>s;
    int sum=0;
    for(int i=0;i<s.size();i++)
    {
        if(s[i]=='A') sum+=1;
        else if(s[i]=='1') sum+=10;
        else sum+=s[i]-'0';
    }
    cout<<sum;
	return 0;
}

4077. k显性字符【思维 贪心 / 二分】

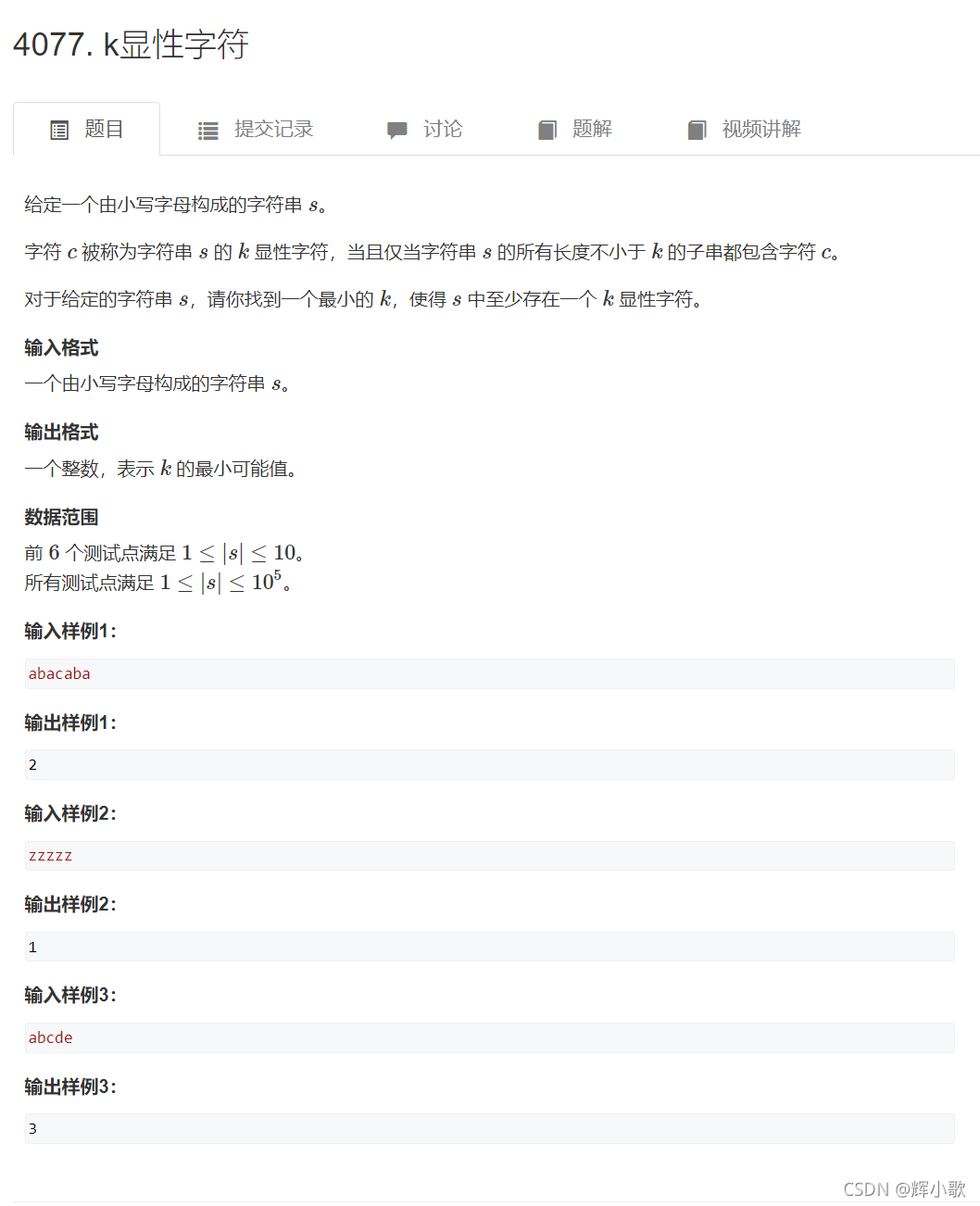
https://www.acwing.com/problem/content/4080/
二分做法:

#include<bits/stdc++.h>
using namespace std;
set<char>st;
string s;
bool check(int k)
{
    for(auto i=st.begin();i!=st.end();i++)//枚举显性字符
    {
       int cnt[30]={0};
       char temp=*i;
       bool flag=0;
       for(int j=0;j<s.size();j++)
       {
           if(j>=k)
           {
               int l=j-k;
               cnt[s[l]-'a']--;
           }
           cnt[s[j]-'a']++;
           if(j>=k-1&&!cnt[temp-'a']) flag=1;
       }
       if(!flag) return true;
    }
    return false;
}
int main(void)
{
    cin>>s;
    for(int i=0;i<s.size();i++) st.insert(s[i]);
    int l=1,r=s.size();
    while(l<r)
    {
        int mid=l+r>>1;
        if(check(mid)) r=mid;
        else l=mid+1;
    }
    cout<<l<<endl;
	return 0;
}

贪心，对于每一个字符求其最大的间距，注意开头和结尾也得特别加。
最后在所有的结果中取一个min即可。

#include<bits/stdc++.h>
using namespace std;
int last[30],maxv[30],n;
string s;
int main(void)
{
    cin>>s;
    s="0"+s;//下标从1开始
    for(int i=1;i<s.size();i++)
    {
        int t=s[i]-'a';
        maxv[t]=max(maxv[t],i-last[t]);
        last[t]=i;
    }
    int n=s.size()-1;
    for(int i=0;i<26;i++) maxv[i]=max(maxv[i],n-last[i]+1);//结尾
    int ans=n;
    for(int i=0;i<26;i++) 
    {
        ans=min(ans,maxv[i]);
    }
    cout<<ans;
    return 0;
}

4078. 01串【DP】

https://www.acwing.com/problem/content/description/4081/
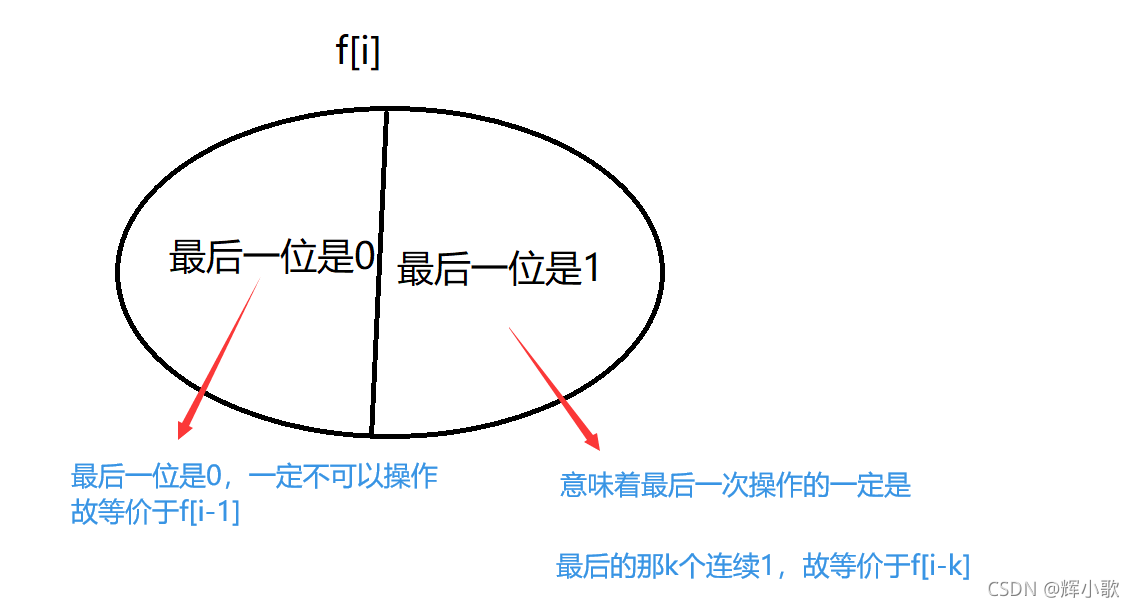
状态表示: f[i] 长度为i 的01串的优秀字符串数量

#include<bits/stdc++.h>
using namespace std;
typedef long long int LL;
const int N=1e5+10;
const int mod=1e9+7;
LL f[N],t,k;
int main(void)
{
    cin>>t>>k;
    for(int i=0;i<N;i++)
    {
        if(i<k) f[i]=1;
        else if(i>=k) f[i]=(f[i-1]+f[i-k])%mod;
    }
    for(int i=1;i<N;i++) f[i]=(f[i]+f[i-1])%mod;//前缀和
    while(t--)
    {
        int l,r; cin>>l>>r;
        cout<<(f[r]-f[l-1]+mod)%mod<<endl;
    }
    return 0;
}