程序要求清单：

基本流程：

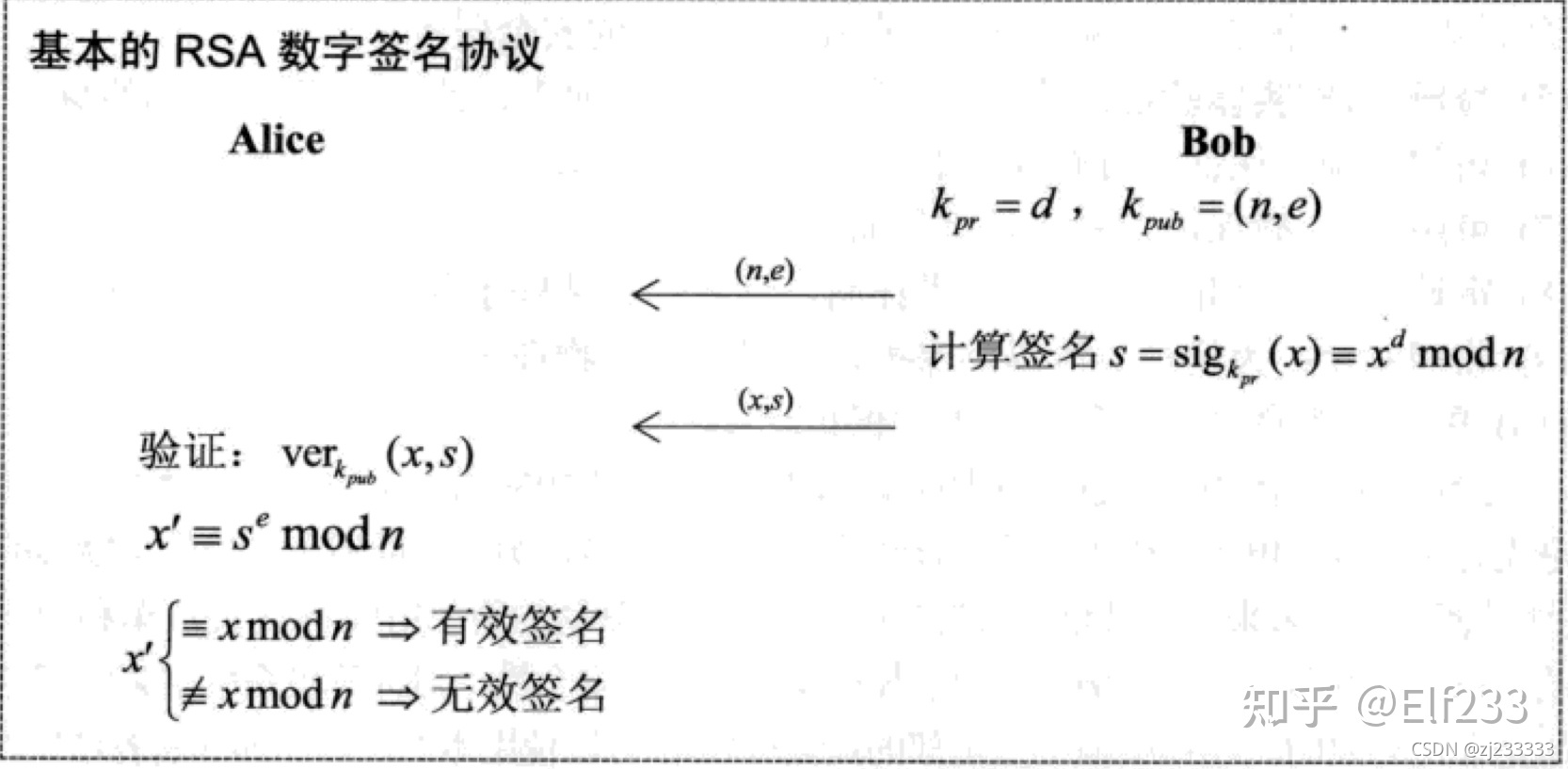
运行结果：

INPUT:
34862844108815430278935886114814204661242105806196134451262421197958661737288465541172280522822644267285105893266043422314800759306377373320298160258654603531159702663926160107285223145666239673833817786345065431976764139550904726039902450456522584204556470321705267433321819673919640632299889369457498214445

OUTPUT:
Private Key:
N: 78841181099223968401000784537446044237784489958930626859661546319915734535564286843929089858806160927583636785213641674742891604758519466416270196149968424211401434194951250003636471951939037856583335344796681676680421749817561884185156901077848451414919839607481314547384942033488032689776582103680101651419
d: 62155833398861149551836037970138554652072353958920365936071774016793504678445192437067806518338650323999067951432452330136982318568982506703216642632242364544915699439246876432122640429532494207894118612299932412964430445703068916755189092721834765176438536555924699728021363703536949347875046151882728437253
Public Key:
N: 78841181099223968401000784537446044237784489958930626859661546319915734535564286843929089858806160927583636785213641674742891604758519466416270196149968424211401434194951250003636471951939037856583335344796681676680421749817561884185156901077848451414919839607481314547384942033488032689776582103680101651419
e: 54379617782319392288508796983156014528426545469465358516629409491913015829046366478896491813056080903568607614496062598318891266649056224190078944747724625447985747390726774036280359056832185917603499408809384176157027477704342977680394354765523168680279688950215134901092221515962361649676202653429692278117
Signature:
s: 71919406352359937084182187510227490541914896613466645529207649594247552008972305126510851689232143019784944438466693655526353672464782061473850818475550335761134900001275567160947332462719877194559692283550511188231994020480408965265818017774491786539810263037297828665666952885117080533173354443950829657265
Verify s of m:
valid
m’ (faked): 76185632416095212195849362379326949631255492531288160212489433749029013809159477234031442742457342006136621757534807192466386195243552371639270795778065774775711134972235456069060155133423454262578532881646543833960203758700964200167278452490427449581011414060671053975994766090766673869892463027013529590471
invalid
s’ (faked): 64886342123697490001106226310357396118874720615188625977759508709028733843402866228754809027591115956249353484164041076852718802175168533537718549149953512673140432858680493424329023049213294957469230294496190453936529669882382633436019205635629312788163444233181192368101923610587237545646774852698003010422
invalid

代码实现：

import random


# 求最大公约数
def gcd(a, b):
    if a < b:
        return gcd(b, a)
    elif a % b == 0:
        return b
    else:
        return gcd(b, a % b)


# 快速幂+取模
def power(a, b, c):
    ans = 1
    while b != 0:
        if b & 1:
            ans = (ans * a) % c
        b >>= 1
        a = (a * a) % c
    return ans


# 快速幂
def quick_power(a: int, b: int) -> int:
    ans = 1
    while b != 0:
        if b & 1:
            ans = ans * a
        b >>= 1
        a = a * a
    return ans


# 大素数检测
def Miller_Rabin(n):
    a = random.randint(2, n - 2)  # 随机第选取一个a∈[2,n-2]
    # print("随机选取的a=%lld\n"%a)
    s = 0  # s为d中的因子2的幂次数。
    d = n - 1
    while (d & 1) == 0:  # 将d中因子2全部提取出来。
        s += 1
        d >>= 1

    x = power(a, d, n)
    for i in range(s):  # 进行s次二次探测
        newX = power(x, 2, n)
        if newX == 1 and x != 1 and x != n - 1:
            return False  # 用二次定理的逆否命题，此时n确定为合数。
        x = newX

    if x != 1:  # 用费马小定理的逆否命题判断，此时x=a^(n-1) (mod n)，那么n确定为合数。
        return False

    return True  # 用费马小定理的逆命题判断。能经受住考验至此的数，大概率为素数。


# 卢卡斯-莱墨素性检验
def Lucas_Lehmer(num: int) -> bool:  # 快速检验pow(2,m)-1是不是素数
    if num == 2:
        return True
    if num % 2 == 0:
        return False
    s = 4
    Mersenne = pow(2, num) - 1  # pow(2, num)-1是梅森数
    for x in range(1, (num - 2) + 1):  # num-2是循环次数，+1表示右区间开
        s = ((s * s) - 2) % Mersenne
    if s == 0:
        return True
    else:
        return False


# 扩展的欧几里得算法，ab=1 (mod m), 得到a在模m下的乘法逆元b
def Extended_Eulid(a: int, m: int) -> int:
    def extended_eulid(a: int, m: int):
        if a == 0:  # 边界条件
            return 1, 0, m
        else:
            x, y, gcd = extended_eulid(m % a, a)  # 递归
            x, y = y, (x - (m // a) * y)  # 递推关系，左端为上层
            return x, y, gcd  # 返回第一层的计算结果。
        # 最终返回的y值即为b在模a下的乘法逆元
        # 若y为复数，则y+a为相应的正数逆元

    n = extended_eulid(a, m)
    if n[1] < 0:
        return n[1] + m
    else:
        return n[1]


# 按照需要的bit来生成大素数
def Generate_prime(key_size: int) -> int:
    while True:
        num = random.randrange(quick_power(2, key_size - 1), quick_power(2, key_size))
        if Miller_Rabin(num):
            return num


# 生成公钥和私钥
def KeyGen(p: int, q: int):
    n = p * q
    e = random.randint(1, (p - 1) * (q - 1))
    while gcd(e, (p - 1) * (q - 1)) != 1:
        e = random.randint(1, (p - 1) * (q - 1))
    d = Extended_Eulid(e, (p - 1) * (q - 1))
    return n, e, d


def Sign(x: int, d: int, n: int) -> int:
    s = power(x, d, n)
    return s


def Verify(s: int, e: int, n: int) -> int:
    x_ = power(s, e, n)
    return x_


if __name__ == '__main__':
    key_size = 512
    p = Generate_prime(key_size)
    q = Generate_prime(key_size)
    n, e, d = KeyGen(p, q)

    # 消息
    x = int(input("Message: "))
    if type(x) != int:
        raise ValueError("Must be an integer!")
    # 签名
    s = Sign(x, d, n)
    # 验证
    x_ = Verify(s, e, n)
    Valid = (x_ == x)

    # Attack
    s_ = random.randint(1, (p - 1) * (q - 1))
    m_ = random.randint(1, (p - 1) * (q - 1))

    # Output
    print("Private Key: ")
    print("N: ", n)
    print("d: ", d)
    print("Public Key: ")
    print("N: ", n)
    print("e: ", e)
    print("Signature: ")
    print("s: ", s)
    print("Verify s of m: ")
    if Valid:
        print("valid")
    else:
        print("invalid")

    print("m' (faked): ", m_)
    if Verify(m_, s, n) == x:
        print("valid")
    else:
        print("invalid")
    print("s' (faked): ", s_)
    if Verify(x_, s_, n) == x:
        print("valid")
    else:
        print("invalid")